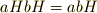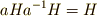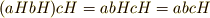商群
正規部分群と群から,剰余類を集めた集合が群になります.これを商群と呼びます.とても大事な群です.
正規部分群の演算
群 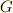 と,その正規部分群
と,その正規部分群 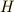 を考えます.
を考えます. 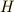 の,
の, 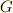 における剰余類を全て集めた集合
における剰余類を全て集めた集合 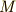 (つまり
(つまり 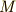 の元のひとつひとつは
の元のひとつひとつは 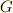 の剰余類)において,二つの剰余類の間に,次のような二項演算を定義します.
の剰余類)において,二つの剰余類の間に,次のような二項演算を定義します.

この演算が確かに一意的だという証明に, 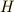 が正規部分群だという点が効いてきます.
が正規部分群だという点が効いてきます. 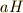 に属する任意の元
に属する任意の元 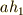 と,
と, 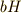 に属する任意の元
に属する任意の元 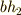 の間には,次の演算が成り立つことが示せるでしょう.途中で,積の順番を自由に入れ替えているのは,
の間には,次の演算が成り立つことが示せるでしょう.途中で,積の順番を自由に入れ替えているのは, 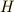 が正規部分群だからです.
が正規部分群だからです.
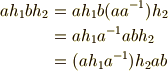
ここで,定義より 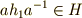 ですから,これに
ですから,これに 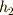 を掛けた
を掛けた 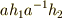 も
も 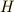 の元です(
の元です( 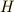 は部分群なので,演算について閉じているはずだからです).従って,全体で
は部分群なので,演算について閉じているはずだからです).従って,全体で 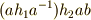 は
は 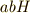 に属していると言えます.確かに,
に属していると言えます.確かに, 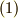 式の二項演算が定義されることが分かりました.
式の二項演算が定義されることが分かりました.
商群
群 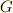 の一つの正規部分群を
の一つの正規部分群を 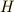 とします.このとき,
とします.このとき, 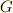 の
の 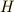 に対する商集合(つまり,
に対する商集合(つまり, 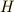 による剰余類全体の作る集合.商集合については, 完全代表系と商集合 を復習して下さい.)を 商群 ,もしくは 因子群 , 剰余群 などと呼びます.記号は商集合と同じで
による剰余類全体の作る集合.商集合については, 完全代表系と商集合 を復習して下さい.)を 商群 ,もしくは 因子群 , 剰余群 などと呼びます.記号は商集合と同じで 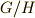 のように書きます.
のように書きます.
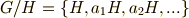
一般の商集合は群にはなりませんが, 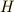 が正規部分群ならば
が正規部分群ならば 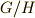 が群になるという点が大事です.前節で示したのは,
が群になるという点が大事です.前節で示したのは, 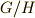 の元同士の演算が閉じている,ということだったのです.単位元(
の元同士の演算が閉じている,ということだったのです.単位元( 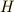 )や,逆元(
)や,逆元( 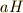 に対して
に対して 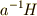 )もありますから,確かに
)もありますから,確かに 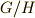 は群です.
は群です.
| [*] | 商群の単位元は 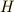 だという点に注意してください. だという点に注意してください. |
| [†] | 商群の各元は 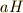 のような形をしています. 準同型写像 を勉強すると『群から群の写像 のような形をしています. 準同型写像 を勉強すると『群から群の写像 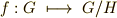 で,元が で,元が 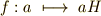 のように移される』というような表現がたくさん出てきます.元の形には のように移される』というような表現がたくさん出てきます.元の形には 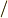 は関係ありません.混乱しないためにも,ここできっちり商群に慣れておきましょう. は関係ありません.混乱しないためにも,ここできっちり商群に慣れておきましょう. |
位数の関係
有限群 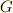 の商群
の商群 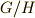 は,
は, 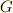 の剰余類の集合です.
の剰余類の集合です. 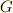 の元の個数より剰余類の種類が多いことは無いので,位数について明らかに次の関係が成り立ちます.
の元の個数より剰余類の種類が多いことは無いので,位数について明らかに次の関係が成り立ちます.

さらに, ラグランジェの定理 より次の関係も言えるでしょう.
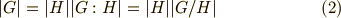
商群の位数は,常に群の位数の約数になっているということです.商群という名前は,式 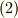 があたかも割り算のように見えることから来ているのでしょう.
があたかも割り算のように見えることから来ているのでしょう.
整数の加群 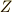 の商群
の商群
練習問題として整数の加群 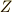 を考えてみます.
を考えてみます. 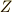 に対し,ある整数
に対し,ある整数  を選びます.
を選びます. 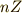 は,
は,  倍数全体を表わす群で,
倍数全体を表わす群で, 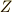 の部分群になります.
の部分群になります.
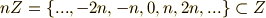
いま, 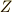 は
は  の剰余で類別できます.剰余類は
の剰余で類別できます.剰余類は ![[m]](./efc831aabf9ade051f781ccb54c2dcdb.png) のように表わします.例えば
のように表わします.例えば ![[3]](./f2577a6fc29b900fe7d4c6321346be48.png) とあるのは『
とあるのは『  で割ったときに余りが3になる数の集合』という意味です.
で割ったときに余りが3になる数の集合』という意味です.
![Z=[0]+[1]+[2]+...+[n-1]](./55c2e61e5d3ec42e15a4ba477e9ba519.png)
商群は,この剰余類を元とする集合 ![\{[0],[1],...,[n-1] \}](./1faa5d4c4598d20480d238882f485759.png) ですから,商群の元の間になりたつ演算を考えるには,これら剰余類同士の合成(この場合は加法)を考えれば良いことになります.
ですから,商群の元の間になりたつ演算を考えるには,これら剰余類同士の合成(この場合は加法)を考えれば良いことになります.
例えば, 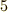 の剰余類を考えているとき,
の剰余類を考えているとき, ![[2]=\{...,-8,-3,2,7,12,... \}](./1c799388cff0fcc47f8054d494f44675.png) と
と ![[4]=\{...,-6,-1,4,9,14,... \}](./7679c6b7684e52fcfc5eb3f196d75a9c.png) を足すと,
を足すと, ![[2]+[4]=\{...,-14,-9,-4,1,6,11,16,21,... \}=[1]](./08a1282a433c17035b411b46fce16f94.png) となります.一般に,剰余類同士の加法には,次の関係がなりたつことが言えそうです.
となります.一般に,剰余類同士の加法には,次の関係がなりたつことが言えそうです.
![[k] + [l] = [k+l] \ {\rm mod.} n](./b36847dfbbfcda8b0e8d141dbcf00b57.png)
この演算規則は,  次の巡回群に成り立つものと全く同じものです( 有限巡回群 参照).よって, Zの商群はn次の有限巡回群に同型である と言えるのです.
次の巡回群に成り立つものと全く同じものです( 有限巡回群 参照).よって, Zの商群はn次の有限巡回群に同型である と言えるのです.