素体
有理数体と剰余体は,それぞれ素体であることを 拡大体 で示しました.実は,逆に全ての素体は有理数体か剰余体のどちらかに同型であることが言えるのです.
theorem
全ての素体は,有理数体 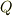 か剰余体
か剰余体 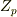 に同型です.
に同型です.
証明には準同型定理と商体の知識が必要です.イデアルも少し出てきます.少し長いですが,証明を掲げておきます.
proof
任意の素体 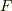 を考えます.乗法の単位元を
を考えます.乗法の単位元を  とすると,
とすると,  の
の 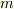 個の和(
個の和( 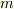 は整数)は
は整数)は 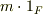 と書けます.ここで,整数
と書けます.ここで,整数 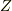 から素体
から素体 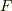 への写像
への写像 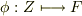 を,
を, 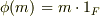 と置くと,
と置くと, 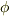 は準同型写像になっています.そこで準同型定理を使うと,
は準同型写像になっています.そこで準同型定理を使うと,  がなりたちますが,
がなりたちますが, 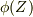 は
は 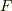 の部分集合ですので,乗法の零元以外に零因子があるはずはなく,整域になります( 整域 参照).すなわち,
の部分集合ですので,乗法の零元以外に零因子があるはずはなく,整域になります( 整域 参照).すなわち, 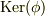 は
は 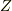 の素イデアルであり,
の素イデアルであり, 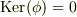 となるか,
となるか, 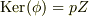 となるか(
となるか( 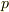 は素数)のいずれかだと言えます.前者
は素数)のいずれかだと言えます.前者 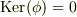 の場合,
の場合,  となります. 両辺の商体を考えると,まず
となります. 両辺の商体を考えると,まず 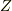 の商体は
の商体は 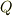 です.また,
です.また, 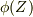 の商体はどんな体だかよく分かりませんが,とりあえず
の商体はどんな体だかよく分かりませんが,とりあえず 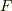 の部分体であることは確かです.
の部分体であることは確かです. 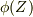 の商体を
の商体を 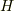 と名づけると,
と名づけると, 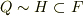 が言えます.ところが
が言えます.ところが 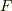 はいま素体ですので,部分体は
はいま素体ですので,部分体は 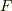 自身しか存在せず,
自身しか存在せず, 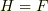 ですので,結局
ですので,結局 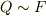 が示せます.
が示せます. 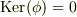 の場合,
の場合, 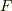 は有理数体
は有理数体 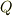 と同型です.同様に,
と同型です.同様に, 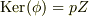 の場合,
の場合,  が示せます.■
が示せます.■
また,次の定理も重要です.
theorem
任意の体 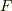 は,ただ一つの素体を含みます.
は,ただ一つの素体を含みます.
proof
前の定理の証明で, 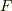 を素体だと仮定しなくても
を素体だと仮定しなくても 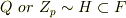 の行までは同じ議論ができますので,任意の体には少なくとも一つは素体
の行までは同じ議論ができますので,任意の体には少なくとも一つは素体 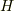 が含まれることは言えます.逆に,含まれる素体は一つしかないことをここから示します.
が含まれることは言えます.逆に,含まれる素体は一つしかないことをここから示します. 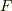 に
に 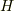 以外の素体
以外の素体 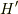 が含まれるとすると,共通集合
が含まれるとすると,共通集合 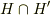 も体であり,
も体であり, 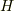 や
や 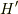 の部分体になるはずです.しかし素体が自分自身以外の部分体を含むことはありませんから,
の部分体になるはずです.しかし素体が自分自身以外の部分体を含むことはありませんから,  が要請されます.すなわち
が要請されます.すなわち 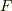 には一つしか素体は含まれません.■
には一つしか素体は含まれません.■
定理と証明だけだと退屈してしまうので,この辺にしておきます.ここで紹介した二つの定理は,とても重要なものですし,定理の意味をよく考えると,体のカラクリが見えてくる部分があると思いますので,もう一度定理の意味を考えてみて下さい. 標数 の記事で,このあたりの話の続きをまた考えます.
補足
ベクトル空間の考え方で素体を考えてみると,あるいは少し見通しが良くなり,素体に対するイメージが湧くかも知れません.
拡大体を体上のベクトル空間と見る見方は,ここまでにもたびたび使って来ました.そこで,ある体 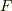 の元も,素体
の元も,素体 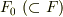 の元
の元 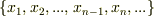 を使って
を使って 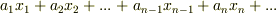 の形で表現できると考えられます.ここに使われている積や和は,当然
の形で表現できると考えられます.ここに使われている積や和は,当然 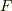 に定義されている『加法』と『乗法』です. 素体は体の最小の部分体ということでしたから,素体はこのベクトル空間の最小の独立なベクトルの集合,つまり基底になっていると考えることが出来ます.
に定義されている『加法』と『乗法』です. 素体は体の最小の部分体ということでしたから,素体はこのベクトル空間の最小の独立なベクトルの集合,つまり基底になっていると考えることが出来ます.