正多面体群1
一つ前の記事で,正六面体群を勉強しました.ここでは,他の多面体群について見ていきます.
正多面体
正多面体には全部で,正四面体,正六面体,正八面体,正十二面体,正二十面体の五種類しかないことが知られています.
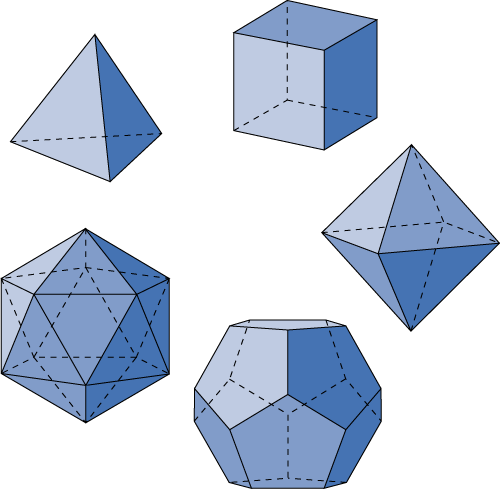
ある正多面体の中心回りの回転で,その正多面体を自分自身に重ね合わせるような回転方法の全体は,群になります.この群を 正多面体群 と呼びます.正多面体の頂点の数,辺の数,面の数を一覧にまとめたのが次の表です.
| 名前(面の数) | 面の形 | 頂点の数 | 辺の数 | 一頂点に集まる面の数 |
|---|---|---|---|---|
| 正四面体 | 正三角形 | 4 | 6 | 3 |
| 正六面体 | 正方形 | 8 | 12 | 3 |
| 正八面体 | 正三角形 | 6 | 12 | 4 |
| 正十二面体 | 正五角形 | 20 | 30 | 3 |
| 正二十面体 | 正三角形 | 12 | 30 | 5 |
正多面体群は, 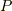 に面の数を加えて表わすことが多いようです.例えば,
に面の数を加えて表わすことが多いようです.例えば, 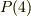 は正四面体群,
は正四面体群, 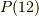 は正十二面体群といった具合です.
は正十二面体群といった具合です.
変換の個数を数え上げる
正六面体を自分自身に重ね合わせる変換には,恒等変換を加えて4種類あることを見ました( 正六面体群 を参照).
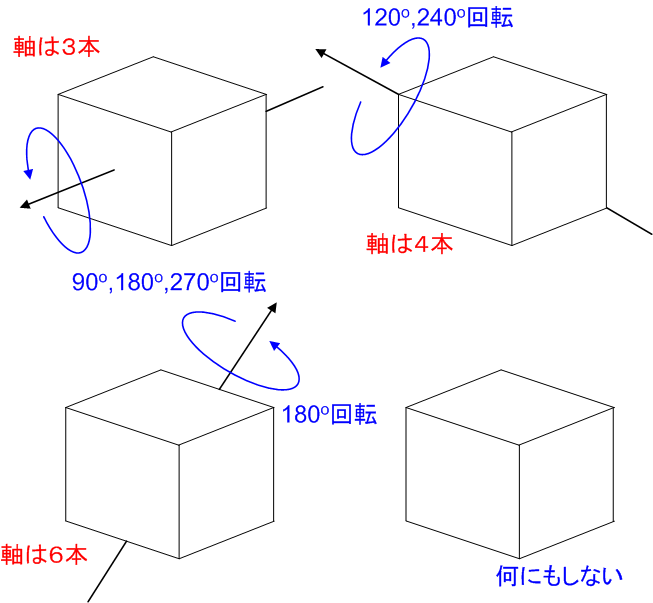
それに加えて,正四面体には,向かい合った一つの頂点と一つの面の中心とを結ぶ軸の回りの回す,という方法があります.これをタイプ5とします.
- なにもしない.(恒等変換)
- 多面体の中心を通り,各面に垂直な軸(
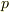 軸)のまわりに回す回転方法(面が何角形をしているかによる.面の持つ頂点の個数を
軸)のまわりに回す回転方法(面が何角形をしているかによる.面の持つ頂点の個数を 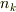 とすると,
とすると, 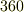 度回すと恒等変換になってしまう分を引いて,
度回すと恒等変換になってしまう分を引いて, 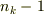 個の種類がある.)
個の種類がある.) - 多面体の中心を通る対角線(
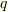 軸)のまわりに回す回転方法(頂点に集まる辺の数(
軸)のまわりに回す回転方法(頂点に集まる辺の数( 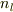 )から,やはり一周すると恒等変換になってしまう分を引き,
)から,やはり一周すると恒等変換になってしまう分を引き, 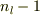 種類がある.)
種類がある.) - 多面体の中心を通り,各辺の中点を通る軸(
 軸)の回りに回す回転方法(
軸)の回りに回す回転方法( 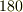 度回す1種類しかない)
度回す1種類しかない) - 多面体の中心を通り,向かい合った一つの頂点と一つの面の中心とを結ぶ軸(
 軸)まわりに回す回転方法(これも面が何角形をしているかによるので,
軸)まわりに回す回転方法(これも面が何角形をしているかによるので, 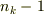 種類ある.)
種類ある.)
各正多面体群の元で,2〜5に対応する軸が何本あるかを表にまとめたのが次表です.表中, 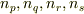 はそれぞれ
はそれぞれ 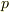 軸,
軸, 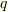 軸,
軸,  軸,
軸,  軸の本数を意味しています.
軸の本数を意味しています.
| 対称軸の総数 | 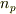 |
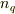 |
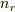 |
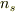 |
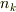 |
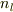 |
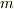 |
|
|---|---|---|---|---|---|---|---|---|
| 正四面体 | 7 | 0 | 0 | 3 | 4 | 3 | 3 | 12 |
| 正六面体 | 13 | 3 | 4 | 6 | 0 | 4 | 3 | 24 |
| 正八面体 | 13 | 4 | 3 | 6 | 0 | 3 | 4 | 24 |
| 正十二面体 | 31 | 6 | 10 | 15 | 0 | 5 | 3 | 60 |
| 正二十面体 | 31 | 10 | 6 | 15 | 0 | 3 | 5 | 60 |
それぞれの多面体群の位数 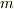 ですが,1〜4のタイプの軸の本数に,それぞれ可能な回点の種類の個数を掛けて全部足すことで求められます.
ですが,1〜4のタイプの軸の本数に,それぞれ可能な回点の種類の個数を掛けて全部足すことで求められます.
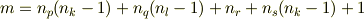
実際に計算してみると, 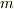 はそれぞれ,
はそれぞれ, 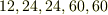 となります.(結果は,すでに表の一番右の欄に書き込んであります.この結果を自分で計算するのは・・・,なかなか骨が折れます(汗).
となります.(結果は,すでに表の一番右の欄に書き込んであります.この結果を自分で計算するのは・・・,なかなか骨が折れます(汗).
この結果は, 正多面体群2 でもう一度考察しますので,何となく覚えておいて下さい.正六面体と正八面体,正十二面体と正二十面体では,何で位数が同じなんだろう?表に出てくる数字が,正六面体と正八面体,正十二面体と正二十面体で,なんだかそれぞれ似てるぞ!?・・・というような色々なことを,上の表を見ながら考えてみるのも,楽しいと思います.この表をプリントアウトして,トイレの壁にでも貼りましょう.
| [*] | 正四面体群に関しては, ときわ台学 さんのページに群表が出ています. 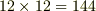 個の組合わせがありますから,これを全部自分で求めるのはとても大変だったと思います.しかし,実際に自分の手を動かして考えるのは非常に大事なことです. 個の組合わせがありますから,これを全部自分で求めるのはとても大変だったと思います.しかし,実際に自分の手を動かして考えるのは非常に大事なことです. |
補足
三次元ユークリッド空間には,ここで取り上げた 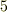 種類の正多面体しかありません.正多面体にはこの
種類の正多面体しかありません.正多面体にはこの 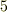 種類しかないことがすでに古代ギリシャで知られていました.プラトン(
種類しかないことがすでに古代ギリシャで知られていました.プラトン( 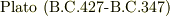 )は,その著書「ティマイオス」(
)は,その著書「ティマイオス」( 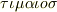 )の中で,哲学者エンペドクレス(
)の中で,哲学者エンペドクレス( 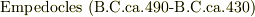 )によって説かれた四元素説(全てのものは水,土,火,空気の四つからなるという説)の四元素に対応させて正多面体を論じています.このため,この五つの正多面体を「プラトンの立体」(
)によって説かれた四元素説(全てのものは水,土,火,空気の四つからなるという説)の四元素に対応させて正多面体を論じています.このため,この五つの正多面体を「プラトンの立体」(  )とも呼びます.
)とも呼びます.
正多面体の頂点の個数( 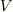 ), 辺の本数(
), 辺の本数( 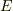 ),面の個数(
),面の個数( 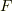 )の間にはオイラーの多面体定理と呼ばれる次の関係が成り立ちます.最初の表を使って,この関係を確認してみてください.
)の間にはオイラーの多面体定理と呼ばれる次の関係が成り立ちます.最初の表を使って,この関係を確認してみてください.

この公式は,少し移項して 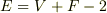 の形にし『線(辺)は,帳面(頂点と面)に引け(
の形にし『線(辺)は,帳面(頂点と面)に引け( 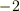 )』と覚えると良いでしょう.
)』と覚えると良いでしょう.
プラトンの正多面体はどの頂点も外側に出っ張っていますので,凸型正多面体とも呼ばれます.これに対し,頂点が凹型でも良いことにすると,ケプラー(  )やポワンソ(
)やポワンソ(  )によって発見された「 ケプラーの多面体 」(
)によって発見された「 ケプラーの多面体 」( 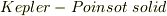 )が,さらに四種類あります.その他,多面体の定義を少し緩くして拡張した,ねじれ多面体,半正多体胞体など,様々な立体が研究されています( 参考 ).四次元以上の正多面体を 多胞体 と呼ぶらしいですが,正多胞体群を考えるという話題も面白そうです.
)が,さらに四種類あります.その他,多面体の定義を少し緩くして拡張した,ねじれ多面体,半正多体胞体など,様々な立体が研究されています( 参考 ).四次元以上の正多面体を 多胞体 と呼ぶらしいですが,正多胞体群を考えるという話題も面白そうです.