体の元の共役と正規拡大体
いよいよこの記事の次はガロア理論に進みます.あと少しです.
体上の元の共役
体  上の代数的な元
上の代数的な元 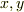 を考えます.この二つの元の最小多項式が等しいとき,
を考えます.この二つの元の最小多項式が等しいとき, 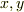 は F上共役である と言います.もしくは『
は F上共役である と言います.もしくは『 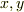 は
は  上の共役元である』のように言います.
上の共役元である』のように言います.
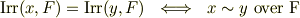
例えば,有理数体  上で
上で 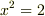 は解を持たず,これ以上の因数分解も不可能ですが,拡大体
は解を持たず,これ以上の因数分解も不可能ですが,拡大体 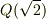 上には解
上には解  を持ちます.このとき,
を持ちます.このとき, 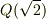 は
は  の代数的拡大体になっていて,
の代数的拡大体になっていて,  の最小多項式は
の最小多項式は 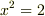 です.よって,定義に従って
です.よって,定義に従って 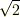 と
と 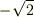 は共役です.
は共役です.
ちょっとイメージが湧いてきましたか?もう一つ例を考えましょう.有理数体  上の二次方程式
上の二次方程式 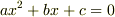 を解の公式を使って解くと,解は一般に
を解の公式を使って解くと,解は一般に 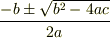 と表されましたが,根号の部分が
と表されましたが,根号の部分が 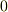 にならないなら,この解は
にならないなら,この解は  の拡大体
の拡大体  上の元です.そして,この二つの解は同一の
上の元です.そして,この二つの解は同一の  上既約な方程式の解ですから,定義より
上既約な方程式の解ですから,定義より  上共役なわけです.そういえば高校の数学でも,このように解の公式を使って解くときにセットで出てくる解を 共役 と呼んでいたような気がします.
上共役なわけです.そういえば高校の数学でも,このように解の公式を使って解くときにセットで出てくる解を 共役 と呼んでいたような気がします.
正規拡大体
元の共役の概念を使って,正規拡大体を定義します.とてもとても大事な概念です.
Important
体  とその代数的拡大体
とその代数的拡大体  を考えます.
を考えます.  の任意の元に対し,その全ての共役元を
の任意の元に対し,その全ての共役元を  が含むとき,
が含むとき,  を
を  の正規拡大体と呼びます.
の正規拡大体と呼びます.
つまり,  を
を  の正規拡大体とするとき,
の正規拡大体とするとき,  上の方程式の解が一つでも正規拡大体
上の方程式の解が一つでも正規拡大体  に含まれるならば,
に含まれるならば,  は同じ方程式の他の解も全て漏れなく含むということです.方程式の解を議論する際,正規拡大体の概念が大事なことが察せられると思います.
は同じ方程式の他の解も全て漏れなく含むということです.方程式の解を議論する際,正規拡大体の概念が大事なことが察せられると思います.
共役や正規拡大体の概念に慣れるために,ここで一つ定理を証明してみましょう.ここまでの知識を総動員すれば簡単に証明できる定理です.頭の体操だと思って,証明を読む前に自分で考えてみてください.
theorem
拡大次数 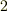 の代数的拡大体は,正規拡大体になります.
の代数的拡大体は,正規拡大体になります.
proof
体  の代数的拡大体を
の代数的拡大体を  とし,
とし, ![[E:F]=2](./8750020a602c2cde9a12e6a52929da77.png) とします.
とします.  は
は  に何か一つだけ代数的元を加えて作られた拡大体だと考えられます.
に何か一つだけ代数的元を加えて作られた拡大体だと考えられます.  には属し,
には属し,  には属さない元
には属さない元 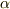 を一つ選ぶと,
を一つ選ぶと, 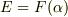 が言え,
が言え, 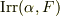 は二次方程式のはずです.そこで
は二次方程式のはずです.そこで 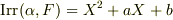 と書き,
と書き, 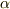 の共役元を
の共役元を 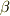 と書くと,解と係数の関係より
と書くと,解と係数の関係より 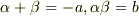 が言え,
が言え, 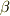 もやはり
もやはり  の元であることが示せます.よって拡大次数
の元であることが示せます.よって拡大次数 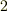 の拡大体は正規拡大体です.■
の拡大体は正規拡大体です.■
正規拡大体と最小分解体の関係
二次方程式を解けば二つの解が,三次方程式を解けば三つの解がセットになって出てきますが,正規拡大体にはこれらの解がどれも含まれるということでした.そこで,体  上の既約な
上の既約な  次方程式
次方程式 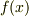 を考えるとき,
を考えるとき,  の正規拡大体
の正規拡大体  は
は 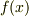 の解を全て含むのですから,
の解を全て含むのですから, 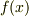 は
は  上で一次式の積に因数分解できると考えられます.
上で一次式の積に因数分解できると考えられます.
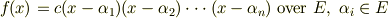
すると,分解体の定義に従い,  は
は 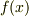 の分解体になっているとも言えるでしょう.実は,
の分解体になっているとも言えるでしょう.実は,  が
が  の有限次正規拡大体であれば,
の有限次正規拡大体であれば,  を最小分解体とする
を最小分解体とする  上の方程式が必ず存在します.
上の方程式が必ず存在します.
| [*] | 色々な言葉が出てきて混乱している人がいると思うので,分解体の定義を復習しておきましょう.  上の多項式 上の多項式 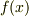 の最小分解体とは, の最小分解体とは, 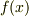 を一次式の積に因数分解できる, を一次式の積に因数分解できる,  の拡大体の中で最小のものです.因数分解の仕方は の拡大体の中で最小のものです.因数分解の仕方は 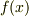 自身によります.解を全て 自身によります.解を全て  上に持っている多項式ならば,そもそも拡大体を考える必要がありませんし, 上に持っている多項式ならば,そもそも拡大体を考える必要がありませんし, 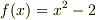 ならば ならば 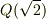 で済むので,複素数体まで拡大する必要はありません.拡大の程度は個々の多項式によるわけです.このように,最小分解体は個々の多項式に応じて一つ決まるものですから, で済むので,複素数体まで拡大する必要はありません.拡大の程度は個々の多項式によるわけです.このように,最小分解体は個々の多項式に応じて一つ決まるものですから,  上の全ての多項式の最小分解体を考えると,最小分解体には 上の全ての多項式の最小分解体を考えると,最小分解体には  自身から複素数体 自身から複素数体 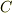 まで,色々なものが出てくるわけです.一方,正規拡大体 まで,色々なものが出てくるわけです.一方,正規拡大体  の定義ではあくまで元が主役です. の定義ではあくまで元が主役です.  の元の最小多項式に対して, の元の最小多項式に対して,  は分解体になっているわけですが,どの程度の拡大体なのかは, は分解体になっているわけですが,どの程度の拡大体なのかは,  の含む元によって決まります.最小分解体にせよ,正規拡大体にせよ,ある多項式をその上で一次式の積に因数分解できる拡大体なわけですが,その定義の出発点がちょっと違うのですね.体 の含む元によって決まります.最小分解体にせよ,正規拡大体にせよ,ある多項式をその上で一次式の積に因数分解できる拡大体なわけですが,その定義の出発点がちょっと違うのですね.体  上には色々な多項式があり,個々の多項式によって最小分解体にも色々あるわけですから, 上には色々な多項式があり,個々の多項式によって最小分解体にも色々あるわけですから,  のある正規拡大体に対し,その正規拡大体を最小分解体とする多項式も存在していそうなものです.次の定理は,この予想を裏付けるものです. のある正規拡大体に対し,その正規拡大体を最小分解体とする多項式も存在していそうなものです.次の定理は,この予想を裏付けるものです. |
theorem
『  は
は  の有限次正規拡大体です』⇔『
の有限次正規拡大体です』⇔『  上の多項式で,
上の多項式で,  を最小分解体とするものが存在します』
を最小分解体とするものが存在します』
proof
(→の証明)  は
は  の代数的拡大体ですので,
の代数的拡大体ですので,  上の代数的な元
上の代数的な元 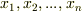 を使って
を使って 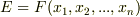 と書けます.
と書けます. 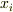 に対応する
に対応する  上の最小多項式を
上の最小多項式を 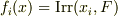 と書くことにし,これらの積を
と書くことにし,これらの積を 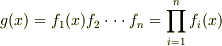 と置きます.個々の最小多項式は
と置きます.個々の最小多項式は  上,
上, 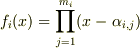 と因数分解できるはずです.
と因数分解できるはずです.  は
は  の
の 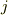 番目の解を意味するとします.これより
番目の解を意味するとします.これより 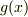 は
は  上で
上で  と表現できます.これは
と表現できます.これは 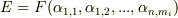 の形の拡大体と見ることができますので,
の形の拡大体と見ることができますので,  は
は 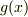 の最小分解体になっています.■
の最小分解体になっています.■
逆の証明はやや難しく,今までに紹介していない定理を含みますので,とりあえず今は証明の方針だけを示すにとどめます.厳密に興味のある人は,適当な代数の教科書を参考にして自分で調べるようにして下さい.
proof
(←の証明の方針)  上の任意の元
上の任意の元  に対し,その
に対し,その  上の共役元
上の共役元 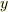 を考えます.
を考えます. 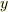 は
は 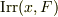 の最小分解体
の最小分解体  に属するのは確かです.いま,
に属するのは確かです.いま, 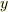 が
が  には属さないと仮定するため
には属さないと仮定するため  とします.
とします.  は
は 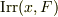 の
の  上の最小分解体であり,
上の最小分解体であり,  は
は 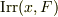 の
の  上の最小分解体になっています.
上の最小分解体になっています.  上共役な元
上共役な元 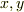 に対し,
に対し, 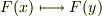 を満たす同型写像
を満たす同型写像  が存在しますが,この同型写像は
が存在しますが,この同型写像は 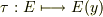 という単射準同型写像にまで拡張できます(これは要証明).一般に
という単射準同型写像にまで拡張できます(これは要証明).一般に  上の多項式の最小分解体
上の多項式の最小分解体 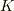 を,その拡大体
を,その拡大体 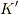 に移す
に移す  上の単射準同型写像
上の単射準同型写像 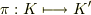 があれば,
があれば, 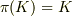 が成り立つことが知られています(これも要証明)ので,
が成り立つことが知られています(これも要証明)ので,  が示せて,
が示せて, 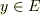 であり,
であり,  は正規拡大体であることが示せます.□
は正規拡大体であることが示せます.□