ラグランジェの定理
ここまでに,群の位数と,元の位数という,紛らわしい二つの言葉が出てきました.混乱しやすいので,もう一度定義をおさらいします.
- 群の位数とは,群の元の数です.
- 元の位数とは,群のある元を生成元として有限部分巡回群がつくれるとき,その部分巡回群の位数のことです.
では,先に進みましょう.
ラグランジェの定理
有限群 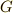 の位数と,その部分群
の位数と,その部分群 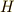 の位数の間には,ラグランジェの定理と言われる美しい関係が成り立っています.
の位数の間には,ラグランジェの定理と言われる美しい関係が成り立っています.
theorem
群 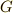 の部分群の位数は,
の部分群の位数は, 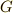 の位数の約数になる.
の位数の約数になる. 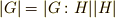 .
.
proof
群 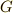 の部分群
の部分群 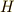 による類別が
による類別が 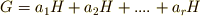 のように表わされるとします.
のように表わされるとします. 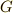 は有限群なので,有限個(
は有限群なので,有限個(  個としています)の類によって類別できるはずです.そこで位数について
個としています)の類によって類別できるはずです.そこで位数について 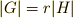 の関係が言えます.
の関係が言えます.  を
を 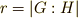 と書くのでしたので,
と書くのでしたので, 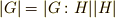 が言えます.■
が言えます.■
証明中では,当たり前と考えて言及しませんでしたが,各類に含まれる元の個数が 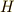 の位数に等しいことが本質的に重要です.
の位数に等しいことが本質的に重要です. 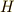 から
から 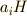 の元を作る
の元を作る 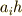 という演算は一意的なので,
という演算は一意的なので, 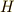 の元と
の元と 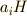 の元の間には一対一対応が成り立ち,元の個数は同じになるわけです.このあと軌道や中心という概念を勉強するとき,ラグランジェの定理が重宝しますので,覚えておくと良いでしょう.
の元の間には一対一対応が成り立ち,元の個数は同じになるわけです.このあと軌道や中心という概念を勉強するとき,ラグランジェの定理が重宝しますので,覚えておくと良いでしょう.
| [*] | 実は 剰余類2 で紹介した指数の定理 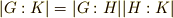 において において 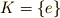 と置けばラグランジェの定理になります. と置けばラグランジェの定理になります. |
| [†] | ラグランジェの時代には群論はまだ完成していませんでしたが,既に幾つかの具体的な例について,ラグランジェはこの定理に気が付いていたということです.恐るべき慧眼です. |
| [‡] | このあたりの記号にまだ慣れていない人は,もう一度 剰余類 や 完全代表系と商集合 の記事を復習してください. |

(群論が生まれる前から群の概念に到達していたラグランジェ)
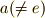 を生成元として,巡回部分群
を生成元として,巡回部分群 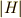 は
は 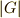 の約数となるはずですが,
の約数となるはずですが, 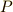 とする)ですから,
とする)ですから, 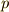 か
か 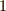 しかあり得ません.しかし,
しかあり得ません.しかし,  と
と  が含まれますので
が含まれますので 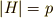 が言えます.
が言えます. 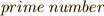 と言うので,その頭文字から来ています.
と言うので,その頭文字から来ています.