類別
群の元を,さらに小さな部分集合に分けることで,色々な種類の元が混じっている群を自分の好みに合わせて小分けし,問題が簡単になることがあります.類別とは,そのような元の分類です.
類別
一般に,集合 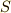 の元
の元 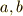 の間に,同値関係(
の間に,同値関係( 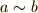 )と呼ばれる関係が定義されているとします.
)と呼ばれる関係が定義されているとします. 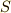 の元のうち,
の元のうち,  と同値関係にある元は全て『
と同値関係にある元は全て『  の仲間』と見なされます.逆に,
の仲間』と見なされます.逆に,  と同値関係にない元は
と同値関係にない元は  の仲間ではありません.
の仲間ではありません.
このようにして,集合 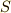 は
は  と同値関係にある元と,同値関係にない元とに,完全に二分することができます.全ての元は,必ず
と同値関係にある元と,同値関係にない元とに,完全に二分することができます.全ての元は,必ず  と同値であるか同値でないかなので,
と同値であるか同値でないかなので, 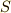 はきれいに過不足無く二つに割れます.このようにして分割した各組を 集合Sの類 と呼びます.また,このような組み分けを 類別 と呼びます.集合
はきれいに過不足無く二つに割れます.このようにして分割した各組を 集合Sの類 と呼びます.また,このような組み分けを 類別 と呼びます.集合 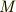 が
が  個の類
個の類 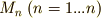 によって類別できる場合,これを和集合と積集合の記号を使って次のように表現できるでしょう.
によって類別できる場合,これを和集合と積集合の記号を使って次のように表現できるでしょう.
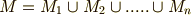
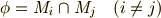
集合の和や共通部分は  や
や 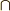 を使って表現するのが正しい表記法ですが,群の類別に関しては慣用的に,普通の
を使って表現するのが正しい表記法ですが,群の類別に関しては慣用的に,普通の 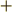 を使って
を使って 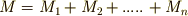 のように書くことが多いようです.
のように書くことが多いようです.
類には,どのようなタイプの同値関係に従って類別を行うかによって,剰余類,共役類などの種類があります.
| [*] | 類別は,集合の元を過不足なく切り分けるという作業です.群を類別したとき,それぞれの類は一般に群にはなりません. |
| [†] | 同値条件とは,二者択一を迫って,全てのものを仲間と非仲間に分けるようなものです.例えば,全ての人は『東京生まれ』か『東京生まれではないか』に二分できます.質問は何でも良いのです.とにかく『条件を満たすか』『それ以外か』というように分けてしまうことです.しかし,単に集合を二つに切り分けるだけでは,あまり面白くありません.ある元と同値のもので一つの類,ある元と同値のものでもう一つの類,というようにして,幾つかの類を作り,過不足無く集合を綺麗に類別できたとき,集合の構成や働きが見通しよく分かるようになるのです.オーケストラは『バイオリン奏者を同値とみなす同値関係』『チェロ奏者を同値とみなす同値関係』等々を導入することで,パート別に奏者を類別できます.『弦楽器』『木管楽器』『金管楽器』などセクション別の類別もできます.各パートは,演奏中は異なる楽譜を演奏していますが,似た役割の楽器をグループ分けすることで,音楽の仕組みをより分かりやすく捉えられるようになります. |
(たくさんの奏者がいるけれど,弦楽器,木管,金管,打楽器など,幾つかのセクションに分けられる.みんなで一つのオーケストラだ.)
例1
対称群の元は,偶置換と奇置換とで類別されます.(偶置換だけからなる集合は交代群と呼ばれる群になりました.奇置換だけからなる集合は群にはなりません.単なる集合です.)
例2
ジョーカーを除いたトランプは『黒』か『赤』に類別できます.『スペード』『ハート』『クラブ』『ダイヤ』の四つに類別することもできます.とても綺麗に類別できる例です.
例3
音楽家全体の集合 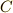 を『上手か』『下手か』で類別するのは難しそうです.中には『どちらとも言えない』という人がいるからです.類別には,もっと厳然とした判断基準を用いる必要があります.
を『上手か』『下手か』で類別するのは難しそうです.中には『どちらとも言えない』という人がいるからです.類別には,もっと厳然とした判断基準を用いる必要があります.
例えば『ウィーン・フィルハーモニー管弦楽団の団員である( 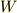 )』『それ以外 (
)』『それ以外 ( 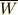 ) 』という分類法を使えば,
) 』という分類法を使えば, 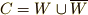 のように類別できます.
のように類別できます.
例4
日本の住所は,47都道府県にきっちり類別できます.
同値関係の定義
類別という概念は,だいたいここまでで理解できたでしょうか?しかし,類別を行うために導入した同値関係という概念については,そのようなものがあると仮定して進めてきましたので,まだ正確に定義していませんでした.同値関係については, 整数の加法群の剰余類 と 剰余類 の記事で,より正確に定義します.