固定部分群
軌道に関する概念で重要なものに,固定部分群があります.
固定部分群の定義
群  の,集合
の,集合 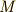 上の軌道を考えるとき,
上の軌道を考えるとき, 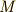 上の一点(
上の一点(  とします)を不動に保つ変換
とします)を不動に保つ変換 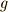 (
( 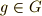 )全体からなる集合は 群になります .群の公理を確認してみましょう.
)全体からなる集合は 群になります .群の公理を確認してみましょう.
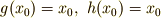 ならば,
ならば,  となり,演算について閉じています.
となり,演算について閉じています.- 結合則がなりたちます.
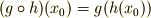
- 単位元があります.
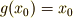 より,
より,  が成り立ちますので,逆元も存在することが言えます.
が成り立ちますので,逆元も存在することが言えます.
これを  の 固定部分群 (もしくは 安定部分群 )と呼び,
の 固定部分群 (もしくは 安定部分群 )と呼び,  のように書きます.例を見たほうが,意味が分かりやすいでしょう.
のように書きます.例を見たほうが,意味が分かりやすいでしょう.
例2
3次の対称群 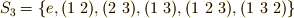 の,集合
の,集合 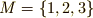 に対する左作用を考えるとき,
に対する左作用を考えるとき, 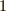 に対する固定部分群は
に対する固定部分群は 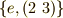 です.また,
です.また, 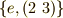 だけで部分群になることを確認してください.
だけで部分群になることを確認してください.
固定部分群と軌道の関係
群  が集合
が集合 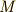 に作用するとき,
に作用するとき, 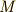 上のある点
上のある点  に関して,
に関して,  の軌道
の軌道 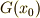 と
と  の固定部分群
の固定部分群 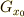 との間には密接な関係があります.(
との間には密接な関係があります.( 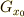 と
と 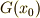 の記号がとても紛らわしいです.ここまでのところを明快に理解してから先に進むようにしてください.軌道
の記号がとても紛らわしいです.ここまでのところを明快に理解してから先に進むようにしてください.軌道 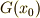 の方は,群を関数のように見ているので括弧がつき,
の方は,群を関数のように見ているので括弧がつき, 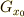 の方は
の方は  の部分群なので
の部分群なので  に添字がついていると覚えると覚えやすいと思います.)
に添字がついていると覚えると覚えやすいと思います.)
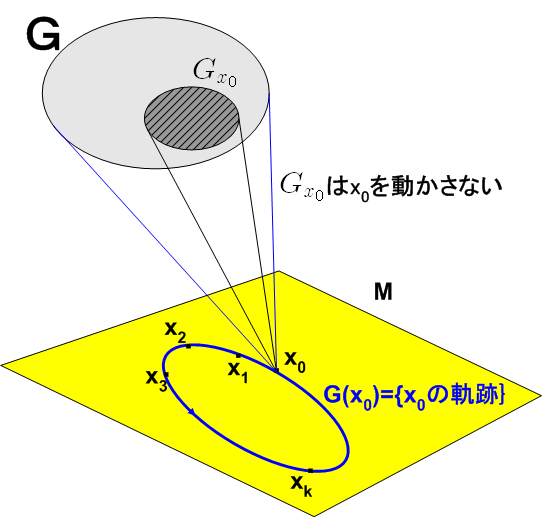
いま,集合  上で点
上で点  の群
の群  による軌道,すなわち
による軌道,すなわち  は,
は,  の部分集合になります.(もし
の部分集合になります.(もし  が不動点なら部分集合は
が不動点なら部分集合は  のみです.もし
のみです.もし  の軌道が
の軌道が 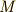 内をくまなく含むとしたら,部分集合は
内をくまなく含むとしたら,部分集合は 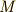 自身です.いずれにせよ,
自身です.いずれにせよ, 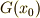 は
は 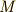 の部分集合だと言えそうです.) いま,
の部分集合だと言えそうです.) いま, 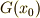 には
には  個の元が含まれるとします.
個の元が含まれるとします.
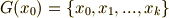
このとき,軌道と固定部分群の間には,次のような重要な関係が成り立つことが知られています.
theorem
群  が集合
が集合 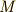 に作用するとき,
に作用するとき, 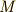 上の一点
上の一点  に関し,
に関し,  の
の  による軌道
による軌道 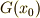 と,
と,  の
の  に関する固定部分群
に関する固定部分群 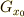 とが一対一に対応します.
とが一対一に対応します.
証明は次のように考えます.軌道 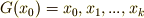 に対し,
に対し,  の元のなかには,
の元のなかには,  を
を 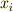 に移すような元が必ず存在するはずです.この元を
に移すような元が必ず存在するはずです.この元を 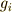 と名づけましょう.さて,ここで仮に
と名づけましょう.さて,ここで仮に  を
を 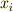 に移すような元が二つあったとします.
に移すような元が二つあったとします.
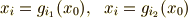
一番目の式から, 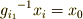 が言えますので,二番目の式の両辺に
が言えますので,二番目の式の両辺に 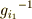 を掛けて次式を得ます.
を掛けて次式を得ます.
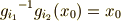
これより, 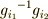 は
は  を動かしませんので,
を動かしませんので,  の固定部分群
の固定部分群 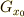 の元だと言うことがわかります.
の元だと言うことがわかります.
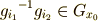
上の関係を,両辺から 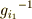 を掛けて次のように書き直してみましょう.
を掛けて次のように書き直してみましょう.
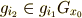
これは,  と
と  が,
が, 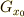 の同じ左剰余類に属しているという主張に他なりません.つまり,群
の同じ左剰余類に属しているという主張に他なりません.つまり,群  の元のうち,軌道
の元のうち,軌道 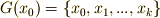 の元
の元  を
を 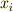 に移すような働きをするものは,全て同じ左剰余類に入るということになります.■
に移すような働きをするものは,全て同じ左剰余類に入るということになります.■
軌道による類別
この結果を使うと『軌道 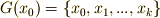 の元
の元  を,どの元に移す作用をもつか』によって,群
を,どの元に移す作用をもつか』によって,群  の元を次のように分類できることになるでしょう.(元
の元を次のように分類できることになるでしょう.(元  を
を 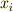 に移すような群
に移すような群  の元の一つを,
の元の一つを, 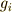 と書いておきます.このような元は複数あるかもしれませんが
と書いておきます.このような元は複数あるかもしれませんが 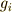 で代表させておきます.)
で代表させておきます.)
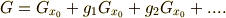
もう一度おさらいしておくと,この式の意味するところは『第一項(  の固定部分群)は,
の固定部分群)は,  を動かさない元全てを含む(これは定義)』『第二項は,
を動かさない元全てを含む(これは定義)』『第二項は,  を
を  に移すような変換をする元全てを含む』『第三項は,
に移すような変換をする元全てを含む』『第三項は,  を
を 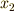 に移すような変換をする元全てを含む』・・・以下同様・・・ということです.
に移すような変換をする元全てを含む』・・・以下同様・・・ということです.
一つの元が,  を
を  に移すこともあれば,気分によって
に移すこともあれば,気分によって 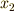 に移すこともある!?・・・なーんてことは,ありませんので,上の分け方に重複はありません.よって,これは 類別 になっているのでした( 軌道の概念 の定理を参照).
に移すこともある!?・・・なーんてことは,ありませんので,上の分け方に重複はありません.よって,これは 類別 になっているのでした( 軌道の概念 の定理を参照).
大事なのは,『群  の元
の元 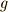 が,
が,  の
の 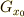 による左剰余類
による左剰余類 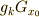 の元である』ということと,『
の元である』ということと,『 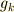 は
は  が
が 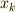 を通るような軌道を与える』ということが同値だという点です.
を通るような軌道を与える』ということが同値だという点です.
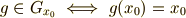
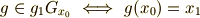

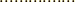
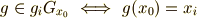
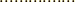
軌道 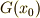 は,
は, 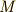 の部分集合なわけですが,その軌道を見ることで,もとの群
の部分集合なわけですが,その軌道を見ることで,もとの群  の元を類別できてしまったわけです.
の元を類別できてしまったわけです.
この結果を次のように表現することもできます.
theorem
群  が集合
が集合 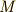 の作用するとき,
の作用するとき, 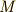 の一点
の一点  のG-軌道は,
のG-軌道は,  の
の 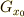 による左剰余類と一対一に対応します.
による左剰余類と一対一に対応します.
また,とくに  が有限群の場合は,次の関係が成り立ちます.
が有限群の場合は,次の関係が成り立ちます.
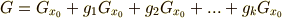
これより, 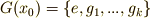 とすると,位数に関して次の関係が言えるでしょう.
とすると,位数に関して次の関係が言えるでしょう.
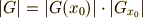
これは大事な関係ですから,定理として覚えておきます.
theorem
有限群  のG-軌道に現われる点の個数は,
のG-軌道に現われる点の個数は,  の位数の約数になります.
の位数の約数になります.
意味するところがとてもイメージしやすい定理です.ここで,自分なりにしっかりと意味を理解しておきましょう.
| [*] | 慣れるまで 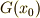 と と 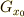 は記号が紛らしいですので,しっかりと覚えるようにしてください. は記号が紛らしいですので,しっかりと覚えるようにしてください. 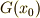 は は  のG-軌道で のG-軌道で 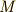 の部分集合, の部分集合, 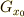 は は  の固定部分群で の固定部分群で  の部分群です. の部分群です. |
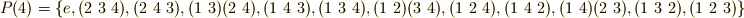 のうち,図の頂点
のうち,図の頂点 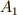 の固定部分群は,
の固定部分群は, 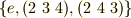 です.
です.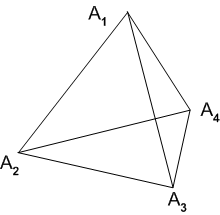
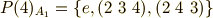
 つの元以外は,頂点
つの元以外は,頂点  が
が 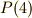 の部分群になっていることを確かめてください.
の部分群になっていることを確かめてください.