軌道の概念
群 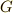 が,集合
が,集合 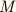 の上で働くという意味を 群が集合の上で働くということ で勉強しました.まずは
の上で働くという意味を 群が集合の上で働くということ で勉強しました.まずは 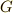 と
と 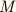 が異なる集合である場合を考えます.
が異なる集合である場合を考えます. 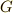 は,何か
は,何か 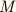 上の点を動かすための関数の集合のようなものです.その作用によって
上の点を動かすための関数の集合のようなものです.その作用によって 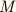 上の点は動かされます.
上の点は動かされます.
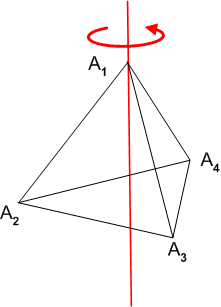
例えば,群 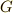 は正八面体を一つの対角線(下図の例では
は正八面体を一つの対角線(下図の例では 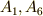 を通る対角線)まわりに回転させ,正八面体自身に重ねる変換を表わす群だとします.
を通る対角線)まわりに回転させ,正八面体自身に重ねる変換を表わす群だとします.
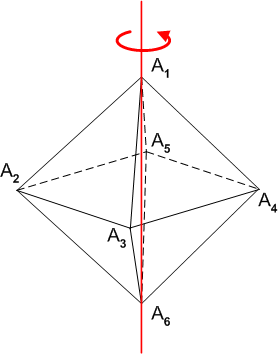
図のように頂点に番号を振ると(頂点 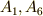 の恒等変換も含めて)
の恒等変換も含めて) 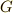 が働いているのは
が働いているのは 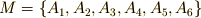 という集合です.頂点
という集合です.頂点 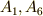 はこの回転によって動きませんが,
はこの回転によって動きませんが,  の元によって
の元によって 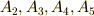 は下図の青い矢印に従った動きをします.
は下図の青い矢印に従った動きをします.
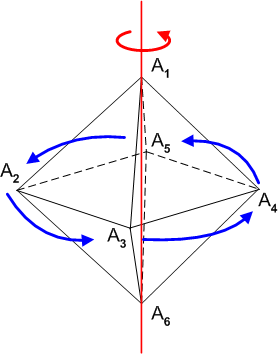
この青い矢印に沿っている点を,頂点 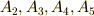 の軌道と呼び,『
の軌道と呼び,『 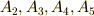 は同じ軌道に属する』と表現することの意味は分かりやすいと思います.軌道は,集合
は同じ軌道に属する』と表現することの意味は分かりやすいと思います.軌道は,集合 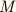 の部分集合になっています.
の部分集合になっています.
軌道のもう少し正確な定義は,次節のように与えられます.抽象的な定義だけから言葉のイメージがピンと来ない場合は,いつでも具体例に戻って考えるようにして下さい.
軌道
集合 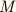 の元
の元  に対し,群
に対し,群 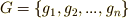 の元が作用するとき,写像は
の元が作用するとき,写像は 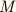 内で閉じていて,結合則がなりたち(
内で閉じていて,結合則がなりたち( 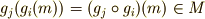 ),
),  の単位元は
の単位元は  を変えない(
を変えない( 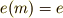 )とします.
)とします.
このとき,ある  に対して,全ての群
に対して,全ての群  の元
の元 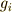 を
を  に作用させた写像
に作用させた写像 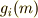 の集合を
の集合を 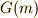 と書き, mによるG-軌道 と呼びます.
と書き, mによるG-軌道 と呼びます.
| [*] | mによるG-軌道が 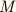 の部分集合になっていることを確認してください. の部分集合になっていることを確認してください. |
| [†] | 数学的にもっとクールに表現すると『群 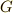 が集合 が集合 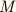 上で働くとき, 上で働くとき,  を を 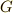 の軌道と定義する』と書けます.少しずつ簡潔な表現にも慣れていきましょう. の軌道と定義する』と書けます.少しずつ簡潔な表現にも慣れていきましょう. |
例1
正四面体群 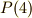 の中で,頂点
の中で,頂点 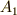 を不動に保つ変化には
を不動に保つ変化には 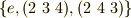 の三つがありました.
の三つがありました.
これは三項の巡回群 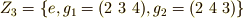 になります. 正四面体の頂点の集合
になります. 正四面体の頂点の集合 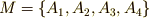 に
に 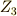 が働く場合を考えます.
が働く場合を考えます. 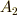 に対して
に対して 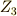 の項を全て作用させると,
の項を全て作用させると, 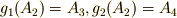 となりますから,この軌道は次のようになります.
となりますから,この軌道は次のようになります.
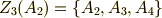
| [‡] | 頂点 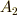 が変換によってどう動いていくかをイメージしてください. が変換によってどう動いていくかをイメージしてください. |
例2
正六角形を中心まわりに平面上で回転させて自身に重ねる六個の変換 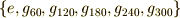 (添字は回転角を表わすとします)のうち,
(添字は回転角を表わすとします)のうち, 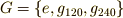 の三つは部分群を作ります.
の三つは部分群を作ります.
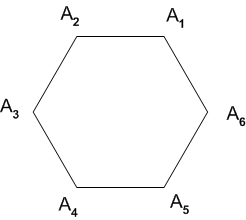
ここで 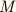 として正六角形の六つの頂点の集合
として正六角形の六つの頂点の集合 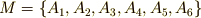 を考えると,軌道は次のようになります(
を考えると,軌道は次のようになります(  度,もしくは
度,もしくは 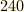 度回転させた先を想像してください).
度回転させた先を想像してください).

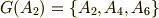
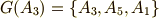
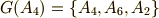

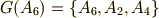
一般的には 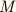 の元の数だけ,軌道がありますが,この例では
の元の数だけ,軌道がありますが,この例では 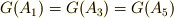 ,
, 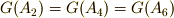 となっているので,独立な軌道は二つだけです.
となっているので,独立な軌道は二つだけです.
| [§] | 軌道の意味を納得しやすい例として  として対称性のある図形を扱いました.最初に軌道の概念が出てきたのも,具体的な図形に群論を利用するところからだと思われます.しかし, として対称性のある図形を扱いました.最初に軌道の概念が出てきたのも,具体的な図形に群論を利用するところからだと思われます.しかし, 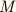 として可能なのは,対称性のある図形ばかりではありません. として可能なのは,対称性のある図形ばかりではありません. |
例3
立方体を,相対する面に垂直な軸を中心として回転させ,立方体自身に移す変換群  を考えます(添字は回転角を表わすとします).
を考えます(添字は回転角を表わすとします).
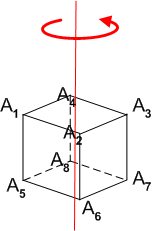
軌道については,次のようになることが分かります.この変換群では,二つの独立な軌道しか出てこないことが分かります.

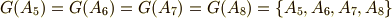
また,図より 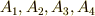 の軌道と
の軌道と 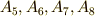 の軌道が交わらないことは明らかでしょう.
の軌道が交わらないことは明らかでしょう.
独立な軌道
軌道に関して次の定理がなりたちます.
theorem
集合 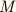 の元
の元 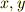 に対し,
に対し, 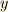 が
が  の G-軌道
の G-軌道 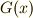 の元でない限り,
の元でない限り, 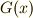 と
と 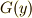 は共通元を持たない.
は共通元を持たない.
この定理は直観的に諒解できます.二つの軌道がもし交わらないなら共通の点はなく,もし二つの軌道が共通の点を持つなら,それは同じ軌道だということです.例2,例3の結果を使って,この定理を確認してみてください.
| [¶] | この定理は非常に重要です.軌道が交わらないということはつまり,各軌道によって集合が類別されるというになります.この記事では例として図形的なものを多く取り上げましたので,軌道のイメージが直観的につかみやすかったと思いますが,一般にはもっと抽象的な集合や群を考えますので,いつも図形的なイメージで軌道を捉えているわけには行きません.抽象的な集合では特に『軌道は群の作用による類別なのだ』とクールに理解しておいた方が良いでしょう.類別を行えることと,同値関係が入っていることは同値な条件でしたが,共役作用に限らず,群の元に作用がある限り,何らかの同値関係がそこに生まれると考えて良いのです. |