群の中心
群 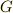 のある元
のある元  が,
が, 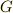 の任意の元
の任意の元  に対して
に対して 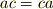 となる場合,
となる場合,  は全ての元と 交換可能 だと言います.この条件を
は全ての元と 交換可能 だと言います.この条件を  と書き直せば,交換可能な元は 自己共役 (自分自身と共役であること)だと言い替えることもできます.
と書き直せば,交換可能な元は 自己共役 (自分自身と共役であること)だと言い替えることもできます.
群 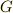 の元と交換可能な元を全て集めた集合
の元と交換可能な元を全て集めた集合 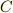 を 中心 と呼びます.
を 中心 と呼びます.
| [*] | 一般に群の演算は非可換ですから,全ての元で 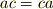 がなりたつことはありません.(むしろ, がなりたつことはありません.(むしろ,  以外で交換可能な元は珍しいはずです.)一方,可換群では 以外で交換可能な元は珍しいはずです.)一方,可換群では 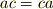 が常になりたちますので, 可換群の中心は可換群自身 になります. が常になりたちますので, 可換群の中心は可換群自身 になります. |
| [†] | 群 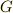 のある共役類に,たった一つの元 のある共役類に,たった一つの元  しか含まれない場合,この しか含まれない場合,この  は, は, 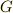 に含まれる任意の元 に含まれる任意の元 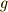 に対して に対して 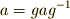 を満たすはずです(もしも を満たすはずです(もしも 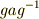 が が  以外になれば,共役類には二つ以上の元が含まれるはずだからです).これは,取りも直さず 以外になれば,共役類には二つ以上の元が含まれるはずだからです).これは,取りも直さず 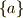 が群 が群 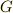 の中心だということです.元を一個しか含まない共役類は常に群の中心になります.群の中心とは, 一個しか元を含まない共役類の和集合だ と考えることもできます. の中心だということです.元を一個しか含まない共役類は常に群の中心になります.群の中心とは, 一個しか元を含まない共役類の和集合だ と考えることもできます. |
中心の性質
一般に,中心は部分群になります.単位元が中心に含まれるのは明らかでしょう.群になる条件として,演算が閉じていることと,逆元も中心に含まれることを以下に示します.
もし群 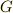 の中心に,単位元でない二つの元
の中心に,単位元でない二つの元 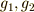 が含まれる場合,中心の定義より,任意の
が含まれる場合,中心の定義より,任意の 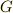 の元
の元 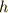 に対して
に対して 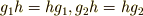 がなりたつはずです.これより次式が言え,
がなりたつはずです.これより次式が言え,  も中心に含まれると言えます.
も中心に含まれると言えます.
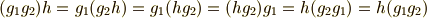
また, 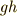 と
と 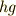 の逆元はそれぞれ
の逆元はそれぞれ 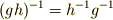 ,
,  ですが,
ですが, 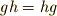 より
より 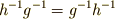 がなりたつことも言え,中心の元の逆元も中心に含まれることが示せました.
がなりたつことも言え,中心の元の逆元も中心に含まれることが示せました.
一般に, 中心は部分群になります .
| [‡] | この次に勉強することですが,中心は他の全てと交換可能なので,ただの部分群ではなく,正規部分群と呼ばれる部分群になります. |
群の位数と中心
群が非可換群ならば,直観的にはいかにも中心には単位元しか含まれないような感じがしますが,そんなことはありません.次の定理があります.
theorem
有限群 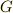 の位数が素数
の位数が素数 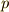 の冪
の冪 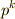 で表わせる場合,
で表わせる場合, 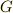 の中心は単位元以外の元を持ちます.
の中心は単位元以外の元を持ちます.
群 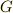 が集合
が集合 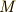 に作用するとき,
に作用するとき, 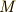 はG-軌道によって過不足なく分けられるのでした(全部で
はG-軌道によって過不足なく分けられるのでした(全部で  個の軌道があるとします.互いに独立なG-軌道は交わらないということと,
個の軌道があるとします.互いに独立なG-軌道は交わらないということと, 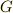 が有限群であることから,一般性を失うことなくこのように仮定できます).
が有限群であることから,一般性を失うことなくこのように仮定できます).
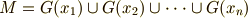
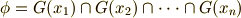
共通集合が無いことより, 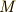 の元の個数についても加法がなりたちます.
の元の個数についても加法がなりたちます.
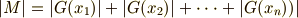
ここまでは軌道の復習です.次に 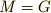 として,
として, 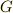 の自分自身に対する作用を見てみます.
の自分自身に対する作用を見てみます. 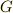 の作用としては,共役作用だけを考えます( 群が集合の上で働くということ 参照).
の作用としては,共役作用だけを考えます( 群が集合の上で働くということ 参照). 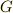 が
が 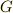 自身の元全てに,共役を取るように作用し,元は軌道ごとに(すなわち共役類ごとに)類別されるわけですが,これらの軌道のうちの幾つかは中心
自身の元全てに,共役を取るように作用し,元は軌道ごとに(すなわち共役類ごとに)類別されるわけですが,これらの軌道のうちの幾つかは中心 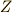 になるはずですから,まとめて
になるはずですから,まとめて 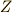 と置けて,次式が書けます.(これを 類方程式 と呼びます.中心は一個しか元を含まない共役類の和集合であることも思い出して下さい.)
と置けて,次式が書けます.(これを 類方程式 と呼びます.中心は一個しか元を含まない共役類の和集合であることも思い出して下さい.)
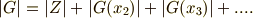
一方, 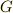 の各元のG-軌道に含まれる元の個数は,
の各元のG-軌道に含まれる元の個数は,  の約数だという定理がありました.
の約数だという定理がありました. 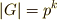 なので,各G-軌道に含まれる元の個数は,
なので,各G-軌道に含まれる元の個数は,  もしくは
もしくは 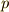 の冪となります.
の冪となります.

もし,中心が単位元だけからなる群だとすると, 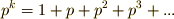 となり,右辺は
となり,右辺は 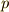 で割れませんから矛盾です.よって,中心は単位元以外の元も持ちます.■
で割れませんから矛盾です.よって,中心は単位元以外の元も持ちます.■
| [§] | 位数が素数 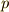 の冪乗である群を" の冪乗である群を" 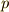 群"と呼びます. 群"と呼びます. |
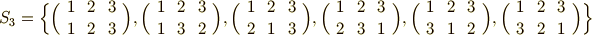
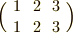 以外に,そのような元はありません.三次の対称群の中心は,単位置換だけだということが分かります.一般に,
以外に,そのような元はありません.三次の対称群の中心は,単位置換だけだということが分かります.一般に, 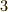 次以上の対称群の中心は,単位置換だけです.
次以上の対称群の中心は,単位置換だけです.