ギリシアの三大作図問題3
ここまでに,作図可能数が体をなすことを見ました.平方根を取る操作をする度に, 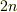 乗根に関係する元が添加されて体は拡大していきます.有理数体から始めて,平方根を取る操作を
乗根に関係する元が添加されて体は拡大していきます.有理数体から始めて,平方根を取る操作を  回行ったときに得られる拡大体を
回行ったときに得られる拡大体を 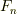 とすると,次のような体の拡大の列が得られます.
とすると,次のような体の拡大の列が得られます. 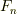 は
は  の
の 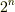 次拡大体です.
次拡大体です.
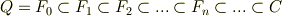
この拡大体の列は無限に続けることができますが,複素数の中には  の解のように作図不能なものも含まれますので,この昇鎖列の上限は
の解のように作図不能なものも含まれますので,この昇鎖列の上限は 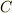 によって評価されます.中間体
によって評価されます.中間体 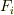 は全て作図可能数体です.
は全て作図可能数体です.
ある数が作図可能かどうかは,『作図したい数が, 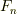 に含まれているか』という問題に帰着しました.
に含まれているか』という問題に帰着しました.
次の節では, 拡大体 で勉強した次数定理を使いますので,忘れてしまった人は,先に進む前に少し復習してください.
![F \subset E \subset D \ \ \Longrightarrow \ \ [D:F]=[D:E][E:F]](./e59bcb6ce6a1e0a3d4f554cbb1423a99.png)
立方体倍積問題
まず立方体倍積問題から始めます.最初の立方体の一辺の長さを  ,体積を
,体積を  とすると,求めたい立方体の辺の長さは,次の方程式の解です.
とすると,求めたい立方体の辺の長さは,次の方程式の解です.

つまり 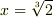 です.
です.  の拡大体
の拡大体 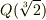 上の数を作図したいわけですが,
上の数を作図したいわけですが,  は三次方程式の解ですから,拡大次数は
は三次方程式の解ですから,拡大次数は 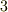 のはずです.(
のはずです.( 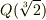 を
を  上のベクトル空間と見れば,基底は
上のベクトル空間と見れば,基底は 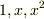 です.)もしも
です.)もしも  が作図可能数であれば,先ほど求めた作図可能数体の拡大列のどこかに
が作図可能数であれば,先ほど求めた作図可能数体の拡大列のどこかに 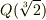 が入っているはずですから,次数定理を使って次式が成り立つはずです.
が入っているはずですから,次数定理を使って次式が成り立つはずです.
![[F_{n}:Q][F_{n}:Q(\root 3\of 2)]=[Q(\root 3\of 2):Q]](./e21c447e50afb87213f611f1f6a9d52d.png)
ところが ![[F_{n}:Q]=2^{n}, [Q(\root 3\of 2):Q]=3](./3652e650cde0956e29587ebd45690db3.png) ですから,このような次数の関係は満たされず,
ですから,このような次数の関係は満たされず, 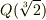 上の数は作図不能であると言えるのです.
上の数は作図不能であると言えるのです.
| [*] | 立法根を添加した体が三次拡大体であることがすぐに分かれば,次数定理を使わなくても明らかだったのですが,少し丁寧に示してみました. |
角の三等分問題
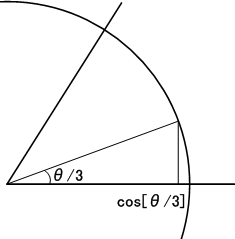
ある角 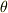 に対し,
に対し, 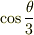 が分かれば,そこから垂線を立てて半径
が分かれば,そこから垂線を立てて半径  の円との交点を求めることによって角を三等分できます.
の円との交点を求めることによって角を三等分できます.
いま  は既知とし,
は既知とし, 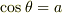 とおくと,
とおくと, 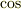 の三倍角の公式
の三倍角の公式 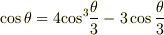 で
で 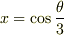 と置くことで,問題は次の方程式の解を作図可能数体の中に求めることへと帰着します.
と置くことで,問題は次の方程式の解を作図可能数体の中に求めることへと帰着します.
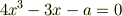
これも三次方程式ですので,立方体倍積問題と全く同じ議論により,解は作図可能数体の 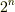 次拡大体には入らないことが示せます.
次拡大体には入らないことが示せます.
円積問題
円積問題は 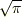 を作図するという問題ですが,この問題の解決はここでは出来ません.
を作図するという問題ですが,この問題の解決はここでは出来ません.  は超越数なので,有理数体の代数的拡大体列に含まれるはずはないのですが,証明は大変に難しいそうです(筆者もどうやるのか知りません).
は超越数なので,有理数体の代数的拡大体列に含まれるはずはないのですが,証明は大変に難しいそうです(筆者もどうやるのか知りません).
| [†] | 定規とコンパスを使った作図法ではありませんが,放物線や双曲線を使えば角の三等分や,倍の体積を持った立方体の辺の長さを求めることが可能です.ヒッピアス(  )は放物線を使って角の三等分法を,アルキタス( )は放物線を使って角の三等分法を,アルキタス(  )は立方体倍積法を示しましたが,これらの方法は何らかの理由により,古代ギリシャ人の美学に反したので幾何学的方法とは認められませんでした.特に政治家や詩人でもあったヒッピアスは,派手好きで威張ったところのあった人のようで,プラトンはヒッピアスの方法に強く反対しました. )は立方体倍積法を示しましたが,これらの方法は何らかの理由により,古代ギリシャ人の美学に反したので幾何学的方法とは認められませんでした.特に政治家や詩人でもあったヒッピアスは,派手好きで威張ったところのあった人のようで,プラトンはヒッピアスの方法に強く反対しました. |