ギリシアの三大作図問題1
しばらく方程式の話ばかりが続きましたので,ここで少し趣向を変えて,定規とコンパスによる作図の話を挟みます.ここまでに勉強してきたことのうち,必要なのは拡大体の概念だけですので,息抜きのつもりで御一読ください.
ギリシャの三大作図問題
古代ギリシャ以来, 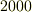 年以上も解決を見なかった次の有名な3つの問題を『ギリシャの三大作図問題』と呼びます.どれも, 定規とコンパスだけをつかって作図せよ という問題です.
年以上も解決を見なかった次の有名な3つの問題を『ギリシャの三大作図問題』と呼びます.どれも, 定規とコンパスだけをつかって作図せよ という問題です.
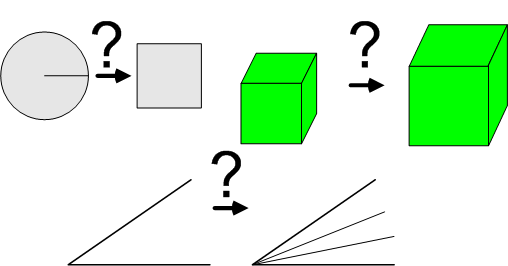
【ギリシャの三大作図問題】
- 円と同じ面積の正方形を作図せよ.
- 与えられた立方体の体積の二倍の体積を持つ立方体を作図せよ.
- 任意の角を三等分せよ.
これらの問題にはそれぞれ『円積問題』『立方体倍積問題』『角の三等分問題』という名前がついています.立方体倍積問題は『デロス島の問題』と呼ばれることもあります.伝説によれば,紀元前 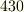 年頃,疫病に悩まされていたアテネの市民が,デロス島のアポロン神の神殿に相談したところ『神殿にある祭壇(立方体)の,ちょうど二倍の大きさの祭壇をつくって奉納すべし』という神託が下りました.人々は最初,各辺をちょうど二倍にした祭壇を奉納しましたが,疫病は一向に収まりません.もう一度神託を聞いてみると,各辺の長さではなく体積をちょうど二倍にしなければならない,とのお告げです.人々は考え付く限りの方法を試しましたが作図に成功せず,疫病はまずます猛威を振るいました.最後に人々は賢人として名高かったプラトンに相談したということです.もちろんプラトンにもこの問題は解けませんでした.ギリシャ三大悲劇作家の一人として知られるエウリピデスの劇中にも,立方体倍積問題に言及するセリフがあったということですから,当時から不可能なことの代名詞として,非常に有名な問題だったのでしょう.(残念ながら,この劇の台本は今日に伝わっていません).
年頃,疫病に悩まされていたアテネの市民が,デロス島のアポロン神の神殿に相談したところ『神殿にある祭壇(立方体)の,ちょうど二倍の大きさの祭壇をつくって奉納すべし』という神託が下りました.人々は最初,各辺をちょうど二倍にした祭壇を奉納しましたが,疫病は一向に収まりません.もう一度神託を聞いてみると,各辺の長さではなく体積をちょうど二倍にしなければならない,とのお告げです.人々は考え付く限りの方法を試しましたが作図に成功せず,疫病はまずます猛威を振るいました.最後に人々は賢人として名高かったプラトンに相談したということです.もちろんプラトンにもこの問題は解けませんでした.ギリシャ三大悲劇作家の一人として知られるエウリピデスの劇中にも,立方体倍積問題に言及するセリフがあったということですから,当時から不可能なことの代名詞として,非常に有名な問題だったのでしょう.(残念ながら,この劇の台本は今日に伝わっていません).

(エーゲ海に浮かぶデロス島.クレオパトラの別荘もあった.)
| [*] | さらに『正七角形を作図せよ』という問題を加えてギリシャの四大作図問題と呼ぶこともあります.デロス島の問題以外の歴史的経緯を知っている方がいらしたら,ご一報ください.正七角形をコンパスと定規で作図することは出来ませんが,その理由は 作図可能な正多角形 で考えます. |
どの問題も一見簡単そうなため,歴史上,様々な人々がこれらの問題に挑戦してきました.三等分問題はヴァンツェル( 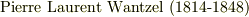 )によって
)によって 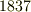 年に,円積問題はリンデマン(
年に,円積問題はリンデマン( 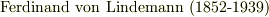 )によって
)によって 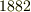 年にようやく解決され,どちらも作図不可能であることが示されました.そして,この初等幾何学の問題を鮮やかに解決したのが抽象代数でした.抽象代数の面目躍如といったところであります.
年にようやく解決され,どちらも作図不可能であることが示されました.そして,この初等幾何学の問題を鮮やかに解決したのが抽象代数でした.抽象代数の面目躍如といったところであります.
立方体倍積問題と角の三等分問題は,ここまでに勉強した拡大体の知識を使って解決できますので,何千年もの間,人類を悩ませてきた問題のドラマチックな解決を,これから見ていきたいと思います.
| [†] | 三大作図問題の意味はどれも分かりやすく,補助線か何かを引けば鮮やかに解決するのではないか?という感じがします.特に,角の三等分なんかは,いかにも出来そうな気がします.そのため,いまだに無数のアマチュア数学愛好家が角の三等分にチャレンジし,数学の学会誌や数学者のところには,毎年膨大な数の自称「作図法」が投稿されてくるということです.もちろんこれらには必ずどこかに間違いが含まれているはずで,例えば,定規やコンパスを次節に定める方法以外の使い方で使ったりしているのですが,中には非常に巧妙な作図法(?)もあり,問題点を発見するのに数時間もかかるようなものまであるそうです.これらの人は『三等分家さん』(英語では 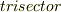 )と呼ばれています.ギリシャ三大作図問題(英語では )と呼ばれています.ギリシャ三大作図問題(英語では  )で検索すると,膨大な数の三等分家さん達のホームページ(トンデモ系?)が引っ掛かりますので,間違い探しを楽しんで下さい. )で検索すると,膨大な数の三等分家さん達のホームページ(トンデモ系?)が引っ掛かりますので,間違い探しを楽しんで下さい. |
| [‡] | 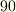 度, 度, 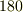 度, 度, 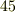 度など,特定の角には三等分可能なものがあります.ある特定の角の三等分にだけ成功し,それで三等分問題を解決したと早とちりしてしまう三等分家さんも多いということです. 度など,特定の角には三等分可能なものがあります.ある特定の角の三等分にだけ成功し,それで三等分問題を解決したと早とちりしてしまう三等分家さんも多いということです. |
定規とコンパスによる作図のルール
まず最初に『定規とコンパスを使って』作図するというのは,次のような手順のみによる作図であると定義します.
- 定規は二点をまっすぐな線で結ぶのに使う.
- コンパスは円を描くのに使う.
- 作図の手順は有限回繰り返すだけとする.
例えば,定規を少しずつずらしながら曲線を描くとか,少しずつコンパスの足を広げていくような使い方は禁じ手です.定規は常に二点を結ぶ線を引くものですから,一点だけを基準に,そこを通る直線を無闇に引いてみるのもダメです.
また,『有限回だけ』という三番目の条件も重要です.もし無限回の作業を繰り返しても良いならば,次のような級数を利用することで  を作図できてしまうでしょう.
を作図できてしまうでしょう.  が作図できれば円積問題は解決できます.しかし,ここでは証明は示しませんが,
が作図できれば円積問題は解決できます.しかし,ここでは証明は示しませんが,  は作図可能数ではありません.
は作図可能数ではありません.
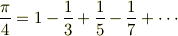
微分の考え方を使えば,連続的変化は無限回の操作で表わせますから,先ほどの,徐々にずらしながら定規やコンパスを使ってはいけない,というルールは三番目の条件にも反すると考えられます.
| [§] | 三等分家の発見する作図法には,どこかに『定規を少しずつずらす』というような連続変化を含む手順が入っていることが多いのです. 折り紙 には角を三等分する方法があるそうですが,これは予め折っておいた線に沿わせて徐々に角を移動させるという連続的操作が含まれているから可能なのです.実は,このような連続変化を含む作図法ならば,古代ギリシャで既にアルキメデスなど,多くの人によって発見・提案されていました. また ギリシャの三大作図問題3 で紹介しますが,放物線を利用して角を三等分する方法も古代ギリシャで既に知られていました.ギリシャの人は,実際に角の三等分が出来なくて困っていたわけではないようなのです.自分たちで決めたルールに基づいた作図という,一種のゲームを楽しんでいたのか,もしくは幾何学に対する何か宗教的な美学に基づき,邪道な作図法(?)を潔しとしなかったのかも知れません. |
さて,平面上に適当に原点を決め,デカルト座標を取るとき,点 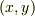 を定規とコンパスで示せるならば,複素数
を定規とコンパスで示せるならば,複素数 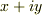 は 作図可能 だと考えることにします.
は 作図可能 だと考えることにします.  平面を複素平面と見ても良いわけですから,実際の紙の上の点と複素数との一対一対応は明らかでしょう.こうして定規とコンパスで示せる点を 作図可能点 と呼び,作図可能点に対応する複素数を 作図可能数 と呼びます. ギリシャの三大作図問題3 .
平面を複素平面と見ても良いわけですから,実際の紙の上の点と複素数との一対一対応は明らかでしょう.こうして定規とコンパスで示せる点を 作図可能点 と呼び,作図可能点に対応する複素数を 作図可能数 と呼びます. ギリシャの三大作図問題3 .
この後,どのような数が作図可能なのか,いよいよ作図可能数の代数的な取り扱いに入ります.( ギリシャの三大作図問題2 へ続く.)