ガロア理論の基本定理
いよいよガロア理論です.ここまでに, 体の自己同型写像 と ガロア群の例 を通じて,体の自己同型写像群(つまりガロア群)というものを考えることで,正規拡大体の拡大次数をガロア群の位数で表すことができ,体の拡大と群という二つの概念が,美しく関係することを勉強しました.この考えを少し発展させると,正規拡大体の列を順次考えていくのに対応して,ガロア群の正規部分群の列が対応するのではないか,と想像できるでしょう.( ガロア群の例 の最後の例に,ガロア群が部分群を持つ例があります.)この記事で考える ガロア理論の基本定理 というのは,そのような体の拡大とガロア群の部分群の関係に関する定理です.今後の話題(作図可能な正多角形だとか,可解な方程式だとか)は,全て,この定理を中心に展開していきます.よく,定理の意味を理解して下さい.
ガロア理論の基本定理
theorem
体 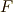 とそのガロア拡大
とそのガロア拡大 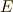 の間に,中間体
の間に,中間体 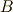 があるとします.このとき,
があるとします.このとき, 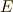 は
は 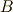 のガロア拡大にもなっており,ガロア群
のガロア拡大にもなっており,ガロア群 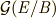 は
は 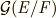 の部分群になっています.また,
の部分群になっています.また, 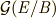 が
が 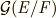 の正規部分群の場合に限り,
の正規部分群の場合に限り, 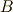 は
は 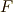 のガロア拡大になります.
のガロア拡大になります.
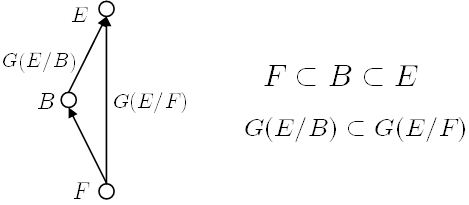
体の包含関係 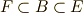 と,群の包含関係
と,群の包含関係 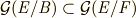 が逆になる点に注意してください.(これを,体と群の包含関係が 反変的 と言ったりします.慣れるまで,一番よく混乱するのは,この反変的包含関係かも知れません.)これは『ガロア理論の基本定理』と呼ばれる大事な定理で,体の昇鎖列と部分群の組成列の関係を示した点が斬新であるだけでなく,中間体が関係している点が秀逸です.
が逆になる点に注意してください.(これを,体と群の包含関係が 反変的 と言ったりします.慣れるまで,一番よく混乱するのは,この反変的包含関係かも知れません.)これは『ガロア理論の基本定理』と呼ばれる大事な定理で,体の昇鎖列と部分群の組成列の関係を示した点が斬新であるだけでなく,中間体が関係している点が秀逸です.
一般に,体とその拡大体があったとき,その中間体にはどのようなものがあるのかを調べるのは容易ではありません.それは,体は一般的に無限集合であることが多く,無数に中間体を決められる可能性があるからです.ところが,拡大体がガロア拡大体である場合に限り,間にある中間体の構造はガロア群の構造に反映され,ガロア群を調べることで中間体の個数や様子をいとも簡単に知ることが出来るわけです.ガロア群はちょうど,中間体を調べるためのモニターのような役割を果たしています.ですから,今後の話題でも,中間体を考えることがとても重要です.このような隠されたカラクリを見破ったガロアの慧眼に,改めて畏怖の念を感じます.
少し長くなりますが,以下に証明を示します.
proof
【 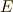 が
が 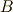 のガロア拡大体であることの証明】拡大体
のガロア拡大体であることの証明】拡大体 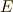 は,
は, 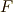 上のある分離多項式の最小分離体になっていますので,
上のある分離多項式の最小分離体になっていますので, 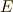 の元
の元 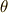 を使って
を使って 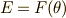 と書けるはずです.このとき
と書けるはずです.このとき  も明らかです.解
も明らかです.解 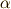 を
を 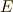 上に持つ,
上に持つ, 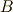 上で既約な多項式
上で既約な多項式 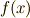 を考えるとき,
を考えるとき, 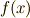 は,
は, 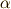 を解に持つ
を解に持つ 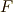 上の多項式
上の多項式 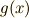 を割るはずです.ここで, ガロア拡大とガロア群 で考えた【補足-1】より,
を割るはずです.ここで, ガロア拡大とガロア群 で考えた【補足-1】より, 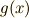 は
は 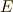 上に全ての解(個数は
上に全ての解(個数は 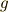 の次数)を持ち,全ての解は相異なります.これより
の次数)を持ち,全ての解は相異なります.これより 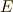 は
は 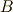 のガロア拡大体になっていると言えます( ガロア拡大とガロア群 の定義
のガロア拡大体になっていると言えます( ガロア拡大とガロア群 の定義 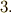 参照).
参照). 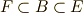 より,
より, 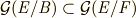 は明らかです.
は明らかです. 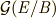 と
と 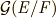 はどちらも
はどちらも 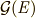 の部分群になっています.■
の部分群になっています.■
proof
【 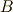 がガロア拡大体→
がガロア拡大体→ 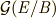 は
は 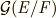 の正規部分群の証明】
の正規部分群の証明】 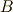 が
が 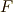 のガロア拡大体ならば,
のガロア拡大体ならば, 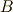 のある元
のある元 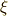 を使って
を使って 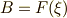 と書けるはずです.
と書けるはずです. 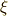 の
の 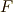 上の最小多項式を
上の最小多項式を 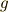 とすると,
とすると, 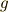 は全ての解を
は全ての解を 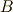 上に持ちます.
上に持ちます. 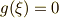 ですが,ある同型写像
ですが,ある同型写像 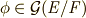 に対して
に対して  を満たすはずですので,
を満たすはずですので,  は
は 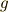 の解の一つで,
の解の一つで, 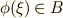 が要請されます.この結果は,
が要請されます.この結果は, 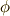 が
が 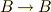 を満たす同型写像だということです.また,
を満たす同型写像だということです.また, 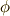 は
は 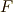 を不動に保ちますので,
を不動に保ちますので, 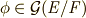 の元で
の元で 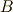 にも属するもの(
にも属するもの( 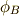 と書きます)は,
と書きます)は, 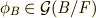 を満たします.これより,写像
を満たします.これより,写像 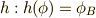 を考えると,
を考えると, 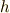 によって
によって 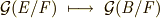 なる写像がなされ,
なる写像がなされ, 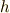 は準同型写像の群になります.準同型定理によって
は準同型写像の群になります.準同型定理によって 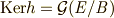 が成り立ちます.準同型写像の核は常に正規部分群ですから,
が成り立ちます.準同型写像の核は常に正規部分群ですから, 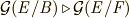 が示されました.■
が示されました.■
proof
【 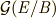 は
は 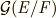 の正規部分群の証明→
の正規部分群の証明→ 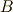 がガロア拡大体】いま
がガロア拡大体】いま 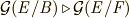 とします.このとき,二つの同型写像
とします.このとき,二つの同型写像 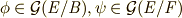 に対し,
に対し, 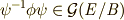 を得ます.
を得ます. 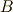 の元
の元 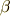 に対し
に対し 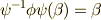 が成り立ちますので,これを変形して
が成り立ちますので,これを変形して  と見ると,
と見ると, 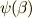 は変換
は変換 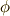 に対して不動を保ち,
に対して不動を保ち, 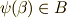 が言えます(
が言えます( 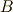 は
は 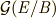 の元に対す固定体でした).ここで,写像
の元に対す固定体でした).ここで,写像 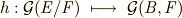 を考えます.
を考えます. 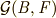 という変な記号を使いましたが,これは『
という変な記号を使いましたが,これは『 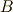 に属する同型写像で,
に属する同型写像で, 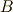 の部分集合
の部分集合 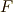 を不動に保つもの』という意味だとします.まだ
を不動に保つもの』という意味だとします.まだ 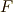 が部分体になることが示せていないので,
が部分体になることが示せていないので, 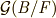 と書くのは早計です.さて, 写像の核は
と書くのは早計です.さて, 写像の核は 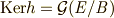 です.いま,第三同型定理( 同型定理 参照)より
です.いま,第三同型定理( 同型定理 参照)より 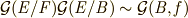 が言えますので,拡大次数について
が言えますので,拡大次数について ![[B:F]=[E:F]/[E:B]=|\cal G \it (E/F)||\cal G \it (E/B)| \le |\cal G \it (B,F)|](./1b6170eb425d38beba7e1a564e78b43c.png) が言えます.一方,
が言えます.一方, 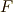 は
は 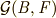 に対する固定体に含まれるはずですので,
に対する固定体に含まれるはずですので, ![[B:F] \ge |\cal G \it (B,F)|](./295104292709f9c96542bc96867c4b60.png) が成り立ちます.従って
が成り立ちます.従って ![[B:F]=\cal G \it (B,F)](./499fa2608254bb999112a9e1c1d99f32.png) あって
あって 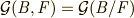 であり,
であり, 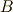 は
は 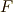 のガロア拡大体になっています.■
のガロア拡大体になっています.■
最後の証明より, 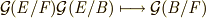 を満たす同型写像の存在が示されます.ふう.
を満たす同型写像の存在が示されます.ふう.