有限巡回群
すでに, 対称群 と 有限回転群 の稿で,巡回群の定義が出てきました.有限回転群や,それに対応する置換操作の作る群は,巡回群だということでした.巡回群の著しい特徴は,全ての元がたった一つの元の冪乗で表わせるという点です.この稿では,巡回群についてもう少し勉強します.新しく出てくる言葉は,部分巡回群,元の位数です.
| [*] | 有限回転群と有限巡回群は,群としては同じと考えてよいもの(同型)なので,これを別々の稿に書いて並べるのはいかにもエレガンスに欠けるかもしれません(ToT)/~. |
有限巡回群
もう一度, 有限回転群 で出てきた,五角形の有限回転群 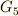 を思い出しましょう.
を思い出しましょう. 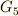 は,位数
は,位数 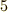 の有限巡回群でした.一般に,図形を
の有限巡回群でした.一般に,図形を 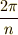 だけ回転する変換を生成元
だけ回転する変換を生成元 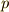 として作られる群は,位数
として作られる群は,位数  の有限巡回群になります.巡回群は
の有限巡回群になります.巡回群は 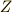 で表わすことが多いようなので,以後,巡回群を表わす記号には
で表わすことが多いようなので,以後,巡回群を表わす記号には 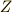 を使います.
を使います.
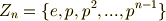
単位元を  で表わしたため,
で表わしたため, 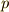 の指数は
の指数は 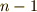 までとなっています.
までとなっています. 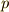 以外の文字を見たくない人は,
以外の文字を見たくない人は,  を
を 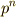 ,もしくは
,もしくは 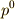 と表わしても良いですが,そうすると単位元があるのかどうか分かりにくくなってしまいますので,やはり上式のように書くのが良いでしょう.
と表わしても良いですが,そうすると単位元があるのかどうか分かりにくくなってしまいますので,やはり上式のように書くのが良いでしょう.
| [†] | 巡回群は一種の対称群ですが,対称群が巡回群になるとは限りません.巡回群は全て可換群ですが,対称群には可換群も非可換群もあるからです. |
指数についての注意
巡回群の元同士の演算では,普通の指数の計算のように,積に対して指数を足すような表記が可能です.便利ですね.
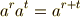
ただし,  次の巡回群には高々
次の巡回群には高々  個の元しかありませんから,もし
個の元しかありませんから,もし 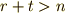 となったら,これはどれか他の元と同じだと言うことになります.注意しないといけません.
となったら,これはどれか他の元と同じだと言うことになります.注意しないといけません.
全ての元を順番に並べてある場合 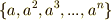 ,
, 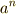 が単位元
が単位元  と等しくなるのですから,
と等しくなるのですから, 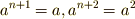 という具合に,
という具合に,  を越えた分だけまた元に戻ります.そこで,指数として
を越えた分だけまた元に戻ります.そこで,指数として 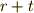 を
を  で割った剰余を考えるようにすれば心配いりません.
で割った剰余を考えるようにすれば心配いりません.

部分巡回群と元の位数
位数  の巡回群
の巡回群 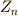 を考えましょう.つまり,
を考えましょう.つまり, 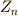 の中には異なる元が
の中には異なる元が  個あるということです.
個あるということです.
ここで, 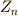 の任意の元を一つ選び(仮に
の任意の元を一つ選び(仮に  と名づけます),
と名づけます),  の冪乗を考えます.
の冪乗を考えます.
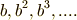
ここで  は有限巡回群
は有限巡回群 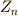 の要素なので,
の要素なので,  の冪乗が無限種類あるということはなく,どこかで出尽くすはずです.全ての種類の出尽くした後の冪乗(
の冪乗が無限種類あるということはなく,どこかで出尽くすはずです.全ての種類の出尽くした後の冪乗( 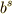 とします)は,それまで出てきた
とします)は,それまで出てきた  の冪乗のどれか(
の冪乗のどれか(  とします)と等しいはずですから,次のように書けます.
とします)と等しいはずですから,次のように書けます.

ここで 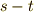 は
は  よりも小さいはずなので,結局,
よりも小さいはずなので,結局,  の
の  乗を
乗を  から
から 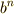 まで順番に見ていく途中に, どこかに単位元が出てくる ということです.
まで順番に見ていく途中に, どこかに単位元が出てくる ということです. 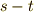 を
を 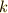 と置くと,一般的には
と置くと,一般的には 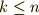 が言えるということです.
が言えるということです.
ここまでの  の冪乗を使って,
の冪乗を使って, 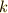 次の巡回群を生成することができます.
次の巡回群を生成することができます.
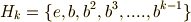
この 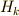 を,
を, 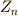 の 部分巡回群 と呼びます.この
の 部分巡回群 と呼びます.この 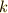 の値は,
の値は, 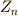 のどの元を生成元として選ぶかによって異なります.逆に,どの元を部分巡回群の生成元とするかを選べば,この
のどの元を生成元として選ぶかによって異なります.逆に,どの元を部分巡回群の生成元とするかを選べば,この 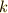 の値は一つに決まります.
の値は一つに決まります.
つまり,巡回群の元の一つ一つは,その元を生成元として作る部分巡回群の位数と一対一に対応しているということです.
この 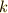 を, 元の位数 と言います.(今後混乱しないように,群の位数との意味の違いをしっかり確認しておいて下さい.)いろいろ書きましたが,要するに群の元
を, 元の位数 と言います.(今後混乱しないように,群の位数との意味の違いをしっかり確認しておいて下さい.)いろいろ書きましたが,要するに群の元  が
が 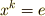 を満たすなら,そのような
を満たすなら,そのような 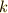 で最小のものを元の位数と呼ぶということです.
で最小のものを元の位数と呼ぶということです.
| [‡] | ここでは,最初に有限巡回群 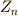 を考えましたが,一般には,ある群(有限群でも無限群でもよい)の元 を考えましたが,一般には,ある群(有限群でも無限群でもよい)の元  を生成元として巡回群が生成されれば,元 を生成元として巡回群が生成されれば,元  の位数を定義できます.また,群有限群に対しては,その元の冪乗は群の中で閉じているはずで,有限種類しかありませんから,もし単位元が含まれれば巡回部分群を作ります.(単位元のみ,もしくは群自身も自明な部分群になりますので,絶対にそのような部分群があると言えます.) ですから,別にもとの群が巡回群である必要は全くありません.上の例では,巡回の意味が分かりやすいように巡回群 の位数を定義できます.また,群有限群に対しては,その元の冪乗は群の中で閉じているはずで,有限種類しかありませんから,もし単位元が含まれれば巡回部分群を作ります.(単位元のみ,もしくは群自身も自明な部分群になりますので,絶対にそのような部分群があると言えます.) ですから,別にもとの群が巡回群である必要は全くありません.上の例では,巡回の意味が分かりやすいように巡回群 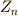 を考えましたが,元の位数は一般の有限群の元に対して定義できる,という点を混乱しないで下さい.元の位数は, ラグランジェの定理 でまた勉強します. を考えましたが,元の位数は一般の有限群の元に対して定義できる,という点を混乱しないで下さい.元の位数は, ラグランジェの定理 でまた勉強します. |
| [§] | もとの群 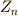 の元を任意に選び,それを生成元として巡回群を作ってみると,一般にはもっと次数の低い巡回群ができてしまう,ということでした.ここで巡回群の定義に立ち戻ってみると, の元を任意に選び,それを生成元として巡回群を作ってみると,一般にはもっと次数の低い巡回群ができてしまう,ということでした.ここで巡回群の定義に立ち戻ってみると, 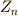 は一つの生成元の冪乗によって作られたわけですから,その生成元の位数は は一つの生成元の冪乗によって作られたわけですから,その生成元の位数は  であるはずです.一般に であるはずです.一般に  次の巡回群の元の中には,位数が 次の巡回群の元の中には,位数が  であるものが存在すると言えます. であるものが存在すると言えます. |
演習問題1
一つの元  を生成元とする有限巡回群は,
を生成元とする有限巡回群は, 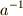 を生成元とする有限巡回群に等しいことを示してください.
を生成元とする有限巡回群に等しいことを示してください.
演習問題2
巡回群は可換群であることを確認してください.
 の有限巡回群の生成元の選び方には何通りあるでしょうか.
の有限巡回群の生成元の選び方には何通りあるでしょうか.