体の自己同型写像
体  から体
から体  自身への同型写像を, 自己同型写像 と言います( 参考 ).体には加法と乗法がありますから,自己同型写像
自身への同型写像を, 自己同型写像 と言います( 参考 ).体には加法と乗法がありますから,自己同型写像 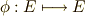 は次の二式を満たすものと定義できます.
は次の二式を満たすものと定義できます.
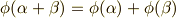
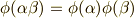
つまり,ここで考えているのは,加法群としての  の自己同型写像と,乗法群としての
の自己同型写像と,乗法群としての 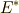 の自己同型写像を,どちらも保つように一つに併せたものです.
の自己同型写像を,どちらも保つように一つに併せたものです.
自己同型写像の群
二つの自己同型写像 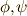 の合成写像
の合成写像 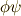 は,やはり自己同型写像になります.また,自己同型写像の逆写像も自己同型写像です.そこで,全ての元を自分自身に移す自己同型写像(つまり恒等写像)を単位元とすれば,
は,やはり自己同型写像になります.また,自己同型写像の逆写像も自己同型写像です.そこで,全ての元を自分自身に移す自己同型写像(つまり恒等写像)を単位元とすれば,  の 自己同型写像全体は群をなします .
の 自己同型写像全体は群をなします .
この群を 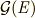 と書きます.
と書きます.
特に,自己同型写像 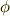 が
が  の部分体
の部分体 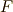 を動かさないとき,すなわち
を動かさないとき,すなわち 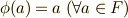 が成り立つとき,
が成り立つとき,  を
を  の 固定体 と呼びます.
の 固定体 と呼びます.
反対に,  の部分体
の部分体  を不動に保つ自己同型写像の集合
を不動に保つ自己同型写像の集合  は,
は, 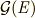 の部分群となります.これを
の部分群となります.これを 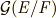 と書くことにします.
と書くことにします. 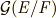 は
は 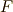 の 固定部分群 になっているわけです.
の 固定部分群 になっているわけです.
自己同型写像の一次独立・一次従属
体  の自己同型写像
の自己同型写像 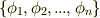 が,
が,  上次式を満たす場合を考えます.
上次式を満たす場合を考えます.
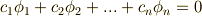
この式が成りたつのが  の場合だけならば,
の場合だけならば, 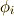 は
は  上 一次独立 だと言います.逆に,上式を満たす
上 一次独立 だと言います.逆に,上式を満たす 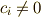 が存在するとき,
が存在するとき, 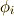 は
は  上 一次従属 だと言います.
上 一次従属 だと言います.
この用語は線形代数からの便宜的な借用で,実際に 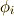 をベクトル空間の元だとは考えない方が良いと思います. 一次独立な自己同型写像は,相異なる ということだけ覚えておきましょう.
をベクトル空間の元だとは考えない方が良いと思います. 一次独立な自己同型写像は,相異なる ということだけ覚えておきましょう.
重要な定理
体の自己同型写像を元とする群を考えました.何でこんな変チクリンな群を考えるのでしょうか?実は,この群を考えると,次に示すように,いままで別々に勉強してきた群論と体論の間に密接な関係が見えてくるのです.ここでは定理を二つ示しますが,最初の定理は二個目の定理を示すための補題です.とても大事な定理なので,少し長くなりますが証明も考えてみてください.
| [*] | ガロア理論とは,正規部分群の列と正規拡大体の列の間にある密接な関係に関するものです.群論と体論は,既習の範囲ではあまり関係なさそうに見えたわけですが,これから,その隠された関係に肉迫していきます.この記事の定理は,そのための第一歩です. |
lemma
体  の相異なる
の相異なる 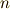 個の自己同型写像
個の自己同型写像  が,
が,  の部分体
の部分体 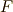 を動かさないとき,
を動かさないとき, ![[E:F] \ge n](./123fb68038b1fdffe349544f15a0c4a9.png) が言えます.
が言えます.
proof
背理法を使って示します.仮に ![[E:F]=r<n](./8bca198dcccd940a49878f9643db1bb3.png) とし,
とし,  を
を 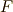 上のベクトル空間と見たときの基底を
上のベクトル空間と見たときの基底を 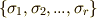 とします.これらを使って,
とします.これらを使って,  本の連立一次方程式
本の連立一次方程式 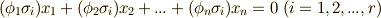 を考えます.この方程式系は,
を考えます.この方程式系は, 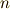 個の未知数
個の未知数 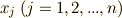 に対して式が
に対して式が  本しかありませんので,
本しかありませんので, 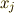 は一次独立ではなく,非零解
は一次独立ではなく,非零解 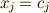 が存在します.一方,
が存在します.一方,  に含まれる任意の元
に含まれる任意の元 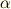 は,適当な係数
は,適当な係数  と基底
と基底 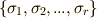 の線形結合で
の線形結合で 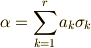 の形に書けますが,任意の
の形に書けますが,任意の 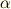 に対して,
に対して, 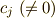 を
を 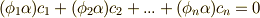 となるように選べます.(
となるように選べます.(  の中に
の中に 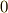 があっても構いませんが,全て
があっても構いませんが,全て 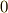 ということはありません.なぜなら
ということはありません.なぜなら  が一次従属だからです.)そこで,
が一次従属だからです.)そこで, 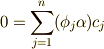 という式を考えてみると,これは次のように変形できます.
という式を考えてみると,これは次のように変形できます. ![0= \sum \limits _{j=1}^{n} ({\phi}_{j} \alpha)c_{j}=\sum \limits _{j=1}^{n} c_{j}[{\phi}_{j}(\sum \limits _{k=1}^{r} a_{k}{\sigma}_{k})]=\sum \limits _{k=1}^{r} a_{k}(\sum \limits _{j=1}^{n} c_{j}({\phi}_{j}{\sigma}_{k})).](./6901795e06b763108a77b3b612153874.png) ここで,左辺
ここで,左辺  より,
より, 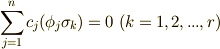 が要請されますが,これは
が要請されますが,これは 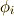 が一次従属という主張に他なりません.これは仮定に反しますので,
が一次従属という主張に他なりません.これは仮定に反しますので, ![[E:F]=r \ge n](./4d43428ae4c54374a8b2d7da0f66289b.png) でなければなりません.■
でなければなりません.■
自己同型写像の群,固定体など,目新しい話題が出てきましたが,次の定理はこれらの間になりたつ,驚くほど美しい結果の一つです.先ほどの定理は,この定理の証明に使うために紹介しました.いままで別々に勉強してきた群と体が,互いに密接に関係していそうだという衝撃の事実を,よく感じてみて下さい.
theorem
体  と,
と,  の自己同型写像の群
の自己同型写像の群 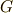 を考えます.
を考えます. 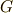 に対する
に対する  の固定部分体を
の固定部分体を 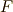 とするとき,
とするとき, ![[E:F]=|G|](./8d2f1171d69e5d071423ab9ecc86735b.png) が成り立ちます.
が成り立ちます.
proof
背理法を使って示します.仮に ![[E:F]=r>n](./6584387d4a6c1c7cdf7d408f29bd35c1.png) とし,
とし,  だとします.また,
だとします.また,  を
を 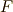 上のベクトル空間と見たときの基底を
上のベクトル空間と見たときの基底を 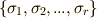 とします.これらを使って,
とします.これらを使って, 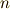 本の連立一次方程式
本の連立一次方程式 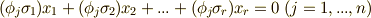 を考えます. この方程式系には,
を考えます. この方程式系には,  個の未知数
個の未知数 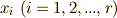 に対して式が
に対して式が 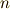 本しかなく,未知数が
本しかなく,未知数が 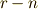 個余計です.よって,
個余計です.よって, 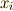 は一次独立ではなく,非零解
は一次独立ではなく,非零解 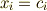 が存在し,
が存在し, 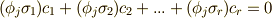 と書けるはずです
と書けるはずです 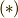 .いま,この
.いま,この 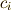 を使って
を使って 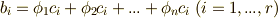 を考えてみると,式
を考えてみると,式 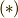 により,
により, 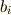 は
は 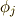 の作用に対して不動だと見ることができますので,定義より
の作用に対して不動だと見ることができますので,定義より 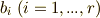 は
は 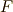 の元だと言えます.これを使うと,
の元だと言えます.これを使うと, 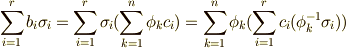 が示せますが,右辺
が示せますが,右辺  より,
より, 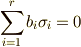 が要請されます.これは
が要請されます.これは 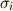 が一次従属という主張であり,問題の条件に反しますので
が一次従属という主張であり,問題の条件に反しますので ![[F:E]=r \le n](./00ebd8672a32b912dbafbfd50f366c11.png) でなければなりません.一方,前定理より
でなければなりません.一方,前定理より ![[F:E]=r \ge n](./29029846f081c73ce4b088de5977bc76.png) ですので,結局
ですので,結局 ![[F:E]=n](./f4cbe625addcf0d7ae79a23a20bb85be.png) が示されます.■
が示されます.■
体  の部分体
の部分体 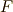 が,
が,  の自己同型写像による有限群
の自己同型写像による有限群 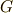 に対して固定部分体になるとします.このとき,
に対して固定部分体になるとします.このとき,  を
を 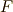 の ガロア拡大体 と呼びます.また,
の ガロア拡大体 と呼びます.また, 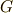 を『
を『  の
の 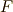 上の ガロア群 』と呼び,
上の ガロア群 』と呼び, 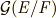 のように書きます.
のように書きます.
いま定めた用語と記号をさっそく使えば,先ほどの定理は ![[E:F]=|\cal G \it (E/F)|](./c5bdd334f4b6b2acfdada2979ac1fa56.png) と書け,『ガロア拡大体の拡大次数は,ガロア群の位数に等しい』と要約できます.なんだか,拡大体の話と群論が急に関係し始めました!
と書け,『ガロア拡大体の拡大次数は,ガロア群の位数に等しい』と要約できます.なんだか,拡大体の話と群論が急に関係し始めました!
| [†] | 体と群が急に一緒に出てきて,面食らっている人がいるかも知れません.何を隠そう(何も隠していませんが),ガロア理論の真髄は,体の拡大を群に結び付けてしまう点にあるのです.群論も体論も無かった 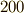 年近くも前に,ガロア拡大とガロア群の関係を見抜いたガロアは,まさに時代を数十年は先取りした超級の天才だったのでしょう.体より群の方が扱いやすく,計算もわかり易いですし,群論の豊富な成果を援用できます.また,体は無限集合であることが多く,無限体の拡大体も無限集合なので,それらの計算は一般に面倒ですが,もしもこれがガロア拡大体ならば,間に有限個の中間体しか存在せず,それらのガロア群を調べることで体の性質を調べることが出来るのです.ガロア群とは,拡大体(往々にして無限体)の構造を,分かりやすいように輪切りにして見せてくれる 年近くも前に,ガロア拡大とガロア群の関係を見抜いたガロアは,まさに時代を数十年は先取りした超級の天才だったのでしょう.体より群の方が扱いやすく,計算もわかり易いですし,群論の豊富な成果を援用できます.また,体は無限集合であることが多く,無限体の拡大体も無限集合なので,それらの計算は一般に面倒ですが,もしもこれがガロア拡大体ならば,間に有限個の中間体しか存在せず,それらのガロア群を調べることで体の性質を調べることが出来るのです.ガロア群とは,拡大体(往々にして無限体)の構造を,分かりやすいように輪切りにして見せてくれる  のようなものです.次の記事では,拡大体の列と,ガロア群の部分群の列が対応していることを見ます. のようなものです.次の記事では,拡大体の列と,ガロア群の部分群の列が対応していることを見ます. |