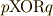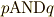体(たい)
ある集合があって,その集合が,四則演算(加法,減法,乗法,除法)に関して閉じているとき,この集合を 体 と呼びます.
体の公理
以下の条件を満たす集合を体と呼びます.
- 加法について可換群になっています.(加法が閉じており,単位元
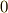 ,逆元
,逆元 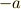 があります).加法の単位元を特に 零元 と呼びます.
があります).加法の単位元を特に 零元 と呼びます. - 乗法について可換群になっています.(乗法が閉じておりる,単位元
 ,逆元
,逆元 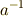 があります.ただし,加法の単位元
があります.ただし,加法の単位元 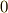 の逆元だけは定義できません.)
の逆元だけは定義できません.) - 加法と乗法について分配法則がなりたちます.
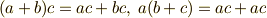
いままで群について学んで来ましたが,群には演算が一種類だけ与えられているのでした(そしてそれは加法でも乗法でも良かったのでした).体には,加法と乗法という,二種類の演算が入っています.加法の逆演算は減法,乗法の逆演算は除法ですから,要するに 体とは四則演算が可能な集合のことである と考えられます.
| [*] | 体は加法に関しては群,乗法に関しても零元を除いて群になっていますので,いままで群論で勉強した概念が,だいたいそのまま体にも当てはまります.また体は,次に勉強する 環 よりも強い構造ですので,環に当てはまる議論が,ほとんどそのまま体に適用できます. |
| [†] | いままで,群論に出てきた情報は一般には非可換でしたが,体の乗法は可換ですので,計算が随分と簡単になることを感じられると思います.体の公理に準じつつも,乗法は非可換の体を「斜体」と呼びます.こんな変な体は,今は覚えなくても大丈夫です. |
例
下の例を考えながら,『四則演算の定義された集合』というのがどういうものか,堪能してみてください.今まで普通に知っていた集合が多いと思いませんか?
例1
有理数の全体は体です.有理数+有理数,有理数-有理数,有理数×有理数,有理数÷有理数(ただし零では割らない)は,いずれも有理数になるからです.これを 有理数体 と呼び, 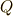 で表わします.
で表わします.
例2
実数の全体も体になります.実数同士は足したり,引いたり,掛けたり,割ったりでき,結果も実数になるからです.同じく 実数体 と呼び, 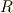 で表わします.
で表わします.
例3
複素数の全体も体になります.自分で確認してみましょう. 複素数体 と呼び, 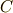 で表わします.
で表わします.
例4
整数の全体は体ではありません.整数÷整数は,かならずしも整数にはならないからです.自然数の全体も体ではありません.自然数-自然数や,自然数÷自然数が,かならずしも自然数にはならないからです.
例6
整数の加法群 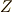 から,素数
から,素数 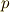 の剰余群
の剰余群 ![Z/[p]](./8f0d1edf3543a46b2ba84710ce748b1c.png) を作ります(
を作ります( ![[p]](./5fcc9b373e17f35dc343b5c9043697d8.png) は
は 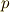 の倍数の集合の意味です.なぜ
の倍数の集合の意味です.なぜ 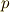 を素数とするのかは後ほど 整域・整数の剰余類の環_ で説明します.)
を素数とするのかは後ほど 整域・整数の剰余類の環_ で説明します.)
![Z/[p]=\{[p],1+[p],2+[p],...,(p-1)+[p] \}](./5ee17662fb97b82fe6c0a44fec6180f6.png)
この元の中で偶数からなる元を 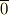 , 奇数からなる元を
, 奇数からなる元を 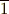 と表わすと,元の間に次のような加法と乗法を定義できます.
と表わすと,元の間に次のような加法と乗法を定義できます.
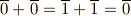
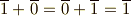
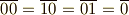
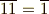
零元は 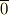 ,乗法の単位元は
,乗法の単位元は 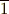 です.このような加法と乗法に対して,
です.このような加法と乗法に対して, ![Z/[p]](./8f0d1edf3543a46b2ba84710ce748b1c.png) は体になります.
は体になります.
例7
例6では,まず具体的に整数の剰余群を考えたので,演算結果も納得し易いものだったと思います.しかし本質的には,例6で考えた演算が内部演算として成り立つ集合は,整数の剰余群に限られる必要はないわけです.そこで例6の結果を,もっとクールに次のように言い換えることができます.
『たった二個の元からなる集合 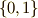 に
に 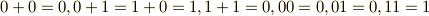 のように演算を定義すれば体になる』
のように演算を定義すれば体になる』
| [‡] | これだけ最初に見ると 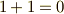 のところで吃驚してしまうと思います.この吃驚の意味するところは深長です.ときに『どうして1足す1は2になるんだ?証明してくれ!』という人や『1足す1が絶対2になるように,答えが一つに決まっているから私は数学が好きです(好きでした)』と言う人に出くわしますが,残念ながら,この手の人は数学の一面しか見ていません.日常, のところで吃驚してしまうと思います.この吃驚の意味するところは深長です.ときに『どうして1足す1は2になるんだ?証明してくれ!』という人や『1足す1が絶対2になるように,答えが一つに決まっているから私は数学が好きです(好きでした)』と言う人に出くわしますが,残念ながら,この手の人は数学の一面しか見ていません.日常, 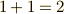 になるのは『そのように演算を定義した体の上で加法を行っていたから』というのが真相なのです.ルールの全く無いゲームは出来ないように,演算にもルールがなくてはなりません."普通の"足し算は,小学校以来慣れ親しんで来ていますので,ルールも何も,当たり前なんじゃないかと思いますが,実は,小学校で習ったのは『 になるのは『そのように演算を定義した体の上で加法を行っていたから』というのが真相なのです.ルールの全く無いゲームは出来ないように,演算にもルールがなくてはなりません."普通の"足し算は,小学校以来慣れ親しんで来ていますので,ルールも何も,当たり前なんじゃないかと思いますが,実は,小学校で習ったのは『 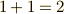 になるようにルールを決めて,ルール通りに計算したらやっぱり になるようにルールを決めて,ルール通りに計算したらやっぱり 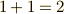 になったよ』という計算練習だったのです.これは証明する対象なのではなくて,単なる約束事です.(サッカーでボールを手で触ってはいけないのは,証明する事柄ではなくて単なるルールです.同じボールでドッヂボールをやるなら手で取らなければなりません.)例6で見た剰余体は実数体とは異なるルールに従う加法・乗法を持っていました.大事なのは,色々なルールがあるんだということを明示的に意識し,いつでも自分がどんなルールに従って(つまりどんな体の上で)計算しているのかを認識することです( 数学に出てくる○○空間ってなんだ? も参照ください). になったよ』という計算練習だったのです.これは証明する対象なのではなくて,単なる約束事です.(サッカーでボールを手で触ってはいけないのは,証明する事柄ではなくて単なるルールです.同じボールでドッヂボールをやるなら手で取らなければなりません.)例6で見た剰余体は実数体とは異なるルールに従う加法・乗法を持っていました.大事なのは,色々なルールがあるんだということを明示的に意識し,いつでも自分がどんなルールに従って(つまりどんな体の上で)計算しているのかを認識することです( 数学に出てくる○○空間ってなんだ? も参照ください). |
| [§] | 上の註は,私達が『数』と呼ぶ集合が,基本的に体であることを念頭に書きました.単に  が が 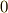 になる演算規則を考えたいだけなら,体でなくとも,環や群でも良いでしょう. になる演算規則を考えたいだけなら,体でなくとも,環や群でも良いでしょう. |
| [¶] | 例7のような演算規則に従って構成される体をブール体と呼びます.ブール体上の計算は全て 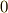 と と 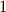 だけになり,計算機理論で応用されています.例6では整数を偶数と奇数に分け,偶数と奇数の演算としてこの演算規則を導入しましたが,実は論理学で使われる真偽表が,まったく同じ規則を満たすのです.下の表は真偽表と呼ばれるもので,例えば一番左の列は『文 だけになり,計算機理論で応用されています.例6では整数を偶数と奇数に分け,偶数と奇数の演算としてこの演算規則を導入しましたが,実は論理学で使われる真偽表が,まったく同じ規則を満たすのです.下の表は真偽表と呼ばれるもので,例えば一番左の列は『文 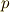 の内容』に従って,真の場合は の内容』に従って,真の場合は 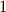 ,偽の場合は ,偽の場合は 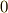 が与えられています.記号 が与えられています.記号 ![p[\rm XOR]q](./6159087388ed57ef8e83492de611dab1.png) は排他的論理和と呼ばれ,『 は排他的論理和と呼ばれ,『 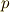 か か 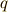 のどちらか一方が真である』ことを意味します(そのため両方が真の場合,この命題は偽になります).記号 のどちらか一方が真である』ことを意味します(そのため両方が真の場合,この命題は偽になります).記号 ![p[\rm AND]q](./71d78be0e5628ecd1ac4b4c9354b156e.png) は論理積と呼ばれ『 は論理積と呼ばれ『 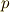 かつ かつ 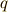 が真である』ことを意味します.さらに興味のある方は,ブール代数,数理論理学,ビット演算などをキーワードに勉強してみてください. が真である』ことを意味します.さらに興味のある方は,ブール代数,数理論理学,ビット演算などをキーワードに勉強してみてください. |
文 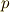 |
文 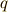 |
||
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
補足
体という概念を最初に導入したのは,デデキント  です.デデキントは『有機的な全体として一つに閉じた集合』という意味合いで,ドイツ語で『人体,体』を表わす
です.デデキントは『有機的な全体として一つに閉じた集合』という意味合いで,ドイツ語で『人体,体』を表わす 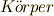 と名づけました.邦訳はそれをそのまま『体』と訳したわけです.(
と名づけました.邦訳はそれをそのまま『体』と訳したわけです.( 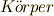 は死体の意味にもなります.)そこで,体を表わす記号に
は死体の意味にもなります.)そこで,体を表わす記号に 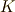 を用いる教科書も多いようです.この用語については,当初からヨーロッパでも「意味が分かりにくい」という批判があったようで,デデキントもわざわざ真意を説明する補足をしたりしています.デデキントは,自律的に独立して運動できる私達の体に,四則演算のできる集合を喩えたようです.とにかく,もう定着してしまった言葉ですから,私達は慣れるしかありません.英語では,
を用いる教科書も多いようです.この用語については,当初からヨーロッパでも「意味が分かりにくい」という批判があったようで,デデキントもわざわざ真意を説明する補足をしたりしています.デデキントは,自律的に独立して運動できる私達の体に,四則演算のできる集合を喩えたようです.とにかく,もう定着してしまった言葉ですから,私達は慣れるしかありません.英語では, 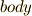 と言わず,
と言わず, 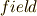 という訳語を当てています.イギリス人は,デデキントの命名が気に入らなかったに違いありません.英米系の教科書では,このため体を
という訳語を当てています.イギリス人は,デデキントの命名が気に入らなかったに違いありません.英米系の教科書では,このため体を 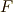 で表すことが多いです.体は,その上でなにか演算を行う土俵となる集合ですから,その意味合いでいくと,
で表すことが多いです.体は,その上でなにか演算を行う土俵となる集合ですから,その意味合いでいくと, 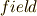 は野原の意味ではなくて,サッカーやラグビーのフィールドのような,何かルールに基づいて試合をする場所の意味に近いかも知れません(用語の成立過程を詳しくしっている人がいたら御一報ください).
は野原の意味ではなくて,サッカーやラグビーのフィールドのような,何かルールに基づいて試合をする場所の意味に近いかも知れません(用語の成立過程を詳しくしっている人がいたら御一報ください).

(数の本質を深く追求し続けたデデキント)