体に関する基本的なこと
体に関して,重要な概念をいくつか紹介します.群論ですでに勉強した内容と重複するトピックも多いでしょう.重要な概念や証明を要するものは,後で再び取り上げる予定ですので,この記事はガイドライン程度に思い,全部理解しようとしなくても大丈夫です.
またこの後,体に関する基本的事柄を順番に漏れなく取り上げることはしません.物理のかぎしっぽ代数分野の当面の目標は,ガロア理論を勉強することですので,そのために必要な最小限の知識を中心に記事は進んでいく予定です.
環やイデアルを体と同時並行的に取り上げる教科書も多くありますが,最初はなるべく環の概念を使わずに議論を進める予定です.
重要な体
幾つかの集合は非常に頻繁に使われるため,記号が慣用的に決まっています.
- 有理数体
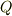
- 実数体
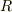
- 複素数体
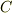
- 体
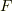 に何か元
に何か元 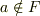 を付け加えるとき,
を付け加えるとき,  を付け加えることでできた新たな体を
を付け加えることでできた新たな体を 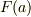 と書きます.(これは『拡大体』と呼ばれるもので,意味については 拡大体 で説明します.)
と書きます.(これは『拡大体』と呼ばれるもので,意味については 拡大体 で説明します.) - 剰余体
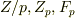 (次節で説明します.)
(次節で説明します.)
整数の剰余体
整数全体 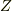 の素数
の素数 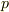 による剰余類
による剰余類 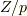 は体になります.これを整数
は体になります.これを整数 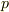 の 剰余体 ,もしくは p分体 と呼びます.剰余体が体になることを,自分で確かめてみてください.
の 剰余体 ,もしくは p分体 と呼びます.剰余体が体になることを,自分で確かめてみてください.
=[a][b+c]=[a(b+c)]=[ab+ac]=[ab]+[ac]=[a][b]+[a][c]](./67b7e49db020cf118b5d12c080b6125e.png)
記号は, 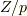 の他に
の他に 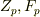 などと書くこともあります.
などと書くこともあります.
| [*] | ちなみに 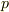 が素数のとき, が素数のとき, 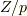 から から 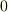 を抜いたものは体にならず,乗法群にしかなりません.記号では を抜いたものは体にならず,乗法群にしかなりません.記号では 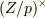 と書き,『 と書き,『 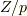 のバチ』と呼んだりします. のバチ』と呼んだりします. |
体と方程式
多項式 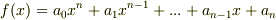 を考えてみましょう.私たちは,
を考えてみましょう.私たちは, 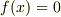 を満たす解
を満たす解  に興味があるわけですが,解は方程式の係数
に興味があるわけですが,解は方程式の係数 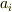 だけによって決まります.(変数が異なる方程式
だけによって決まります.(変数が異なる方程式 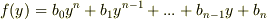 でも,係数に関して
でも,係数に関して 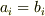 ならば解が等しくなることは明らかでしょう).
ならば解が等しくなることは明らかでしょう).
特に抽象的な方程式論の立場からは,これらの 係数がどの体に含まれるか が非常に重要です.もし係数 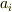 がすべて体
がすべて体 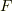 に含まれる数ならば,
に含まれる数ならば, 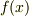 を 体F上の方程式 と言います.
を 体F上の方程式 と言います.
また,方程式の 解がどの体に含まれるか も非常に重要です.例えば方程式 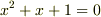 は,有理数体
は,有理数体 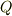 の中には解を持ちません.実数
の中には解を持ちません.実数 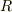 の範囲内にも解を持ちません.ですから,有理数体や実数体上に解を探すならば『解なし』と言うよりほかありません.しかし,もしも解の範囲を複素数体にまで広げて考えれば
の範囲内にも解を持ちません.ですから,有理数体や実数体上に解を探すならば『解なし』と言うよりほかありません.しかし,もしも解の範囲を複素数体にまで広げて考えれば 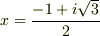 という解が存在します.このように,方程式の『解のある・なし』も,どの体に解を探すかによって変わってくるのです.解が含まれる体を知ることで,方程式の可解性や解の性質が分かったりします.
という解が存在します.このように,方程式の『解のある・なし』も,どの体に解を探すかによって変わってくるのです.解が含まれる体を知ることで,方程式の可解性や解の性質が分かったりします.
先ほどの 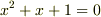 の例に見たように,体
の例に見たように,体 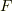 上の方程式(つまり係数が全て
上の方程式(つまり係数が全て 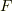 の元である方程式)の解は
の元である方程式)の解は 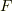 上にあるとは限りませんが,
上にあるとは限りませんが, 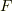 よりも大きな体にまで捜索範囲を広げれば,必ず解が見つかります.最大限,複素数体の範囲にまで捜索範囲を広げれば,必ず解が見つかることが 代数学の基本定理 によって保証されています.私達は方程式を解くことに興味がありますから,このような事情により,今後,方程式論では体の拡大の話題が多くなります.
よりも大きな体にまで捜索範囲を広げれば,必ず解が見つかります.最大限,複素数体の範囲にまで捜索範囲を広げれば,必ず解が見つかることが 代数学の基本定理 によって保証されています.私達は方程式を解くことに興味がありますから,このような事情により,今後,方程式論では体の拡大の話題が多くなります.
極論すれば,抽象的な立場からの方程式論は体論であると言い切っても良いでしょう.
位数
体の元の数を 位数 と呼びます.位数が有限か無限かによって, 有限体 , 無限体 の区別があります.有理数体,実数体,複素数体などは無限体です.
部分体・拡大体・中間体
体 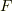 に対し,体
に対し,体 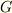 が次の包含関係にあるとき,
が次の包含関係にあるとき, 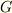 を
を 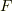 の 部分体 と呼びます.
の 部分体 と呼びます.
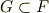
逆に, 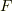 に対し体
に対し体 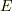 が次の包含関係にあるとき,
が次の包含関係にあるとき, 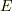 を
を 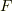 の 拡大体 と呼びます.単に 拡大 と呼ぶこともあります.
の 拡大体 と呼びます.単に 拡大 と呼ぶこともあります.
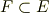
体 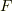 が,
が, 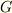 の拡大体であって同時に
の拡大体であって同時に 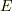 の部分体であるとき,
の部分体であるとき, 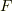 は
は 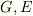 のちょうど中間に位置する体になっています.これを
のちょうど中間に位置する体になっています.これを 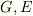 の 中間体 と呼びます.
の 中間体 と呼びます.
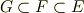
準同型写像・同型写像
準同型写像はすでに群論で勉強したと思います.体は加法と乗法の両方に対して群となりますので,体の準同型 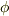 は次の二つの関係を両方満たす必要があります.
は次の二つの関係を両方満たす必要があります.
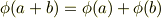
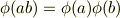
特に,写像が全単射の場合を同型写像と呼ぶことも群論と同じです( 準同型写像 を復習してください).