フェルマーの小定理
群論を整数論に応用して得られる一つの結果として,フェルマーの小定理を見ます.フェルマーの小定理は群論を使わなくても証明できますが,ここまでに勉強した群論の知識を使うと,非常にエレガントに証明できてしまいます.
| [*] | 『 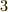 以上の整数 以上の整数  に対し に対し 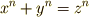 を満たす整数 を満たす整数 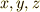 の組は存在しない』という有名なフェルマーの定理と区別するために,こちらの方はフェルマーの小定理と呼ばれます.有名な方は『フェルマーの大定理』もしくは『フェルマーの最終定理』などと呼ばれます.フェルマーの大定理は,長年に渡って証明不可能だと思われていましたが, の組は存在しない』という有名なフェルマーの定理と区別するために,こちらの方はフェルマーの小定理と呼ばれます.有名な方は『フェルマーの大定理』もしくは『フェルマーの最終定理』などと呼ばれます.フェルマーの大定理は,長年に渡って証明不可能だと思われていましたが, 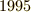 年にワイルズ( 年にワイルズ( 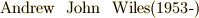 )によって証明されたのは,まだ記憶に新しいところです.歴史上,数多くの数学者がフェルマーの大定理を解決しようと試み,証明にこそ失敗しましたが,その過程で到達した様々な結果や概念によって代数学は大きな進歩を遂げました.さて,私達が勉強するのは小定理の方です. )によって証明されたのは,まだ記憶に新しいところです.歴史上,数多くの数学者がフェルマーの大定理を解決しようと試み,証明にこそ失敗しましたが,その過程で到達した様々な結果や概念によって代数学は大きな進歩を遂げました.さて,私達が勉強するのは小定理の方です. |

(フランスの切手にもなっているフェルマー)
フェルマーの小定理
整数全体 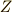 の整数
の整数  の剰余類のうち,
の剰余類のうち, 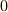 を含む剰余類を除いた集合
を含む剰余類を除いた集合 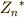 を考えます.このとき,
を考えます.このとき,  を素数(以後
を素数(以後 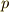 と書きます)とすると,
と書きます)とすると, 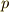 は約数を持ちませんから,
は約数を持ちませんから, 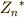 は
は 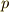 の剰余類によって次のように書けます.
の剰余類によって次のように書けます.
![{Z_{n}}^{*}=\{[1],[2],...,[p-1] \}](./9d86c009345d3dc0ab804053e6cea684.png)
よって,位数は  です.
です.
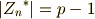
これがフェルマーの小定理です.簡単でしたね!ただし,整数論の教科書に出てくるのは,次の形です.ここまでの議論は,次の定理の証明になっています.
theorem
整数  を,
を, 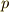 の倍数ではない整数とし,
の倍数ではない整数とし, 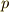 を素数とするとき,
を素数とするとき, 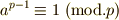 がなりたつ.
がなりたつ.
この定理で何が分かるのか,ちょっと分かり難いかも知れません.例を考えてみれば,なかなか強力な定理だということが分かると思います.
例: 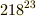 を
を 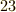 で割った余りを求めてください.
で割った余りを求めてください.
フェルマーの小定理より, 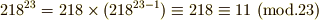 となって,余り
となって,余り 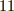 が瞬時に求まります.
が瞬時に求まります.
| [†] | フェルマーの小定理をつかえば,このように,とんでもなく大きな数でも,一瞬で余りが分かってしまいます.素数の判定や暗号理論に欠かせない定理なのです. |
系
フェルマーの小定理を,群論で使いやすい表現に書き直すと次のようになります.
theorem
群 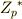 で
で 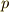 が素数のとき,
が素数のとき, 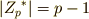 がなりたつ.
がなりたつ.
さらに発展形として,次の定理を考えます.
theorem
群 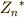 の位数が素数
の位数が素数 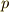 の冪
の冪 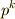 のとき,
のとき, 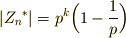 がなりたつ.
がなりたつ.
proof
この場合, 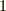 と
と 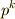 の間にある,
の間にある, 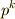 と互いに素であるような数は,
と互いに素であるような数は, 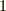 から
から 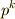 の間にある数のうち,
の間にある数のうち, 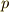 の倍数,
の倍数, 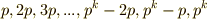 を除いたものです.このような数は,全部で
を除いたものです.このような数は,全部で 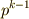 個ありますので,
個ありますので, 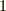 と
と 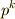 の間にある,
の間にある, 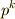 と互いに素である整数は全部で
と互いに素である整数は全部で 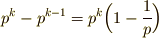 個あると言えます.よって
個あると言えます.よって 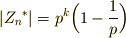 がなりたちます.■
がなりたちます.■
さらに一般の場合には,次のように定理を拡張できます.
theorem
群 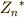 の位数
の位数  が
が 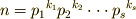 のように素因数分解できるとき,
のように素因数分解できるとき,  がなりたつ.
がなりたつ.
この定理の証明は省略します.これは,このあとに勉強する シローの定理 の一つの表現になっています.