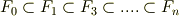拡大体
ある体  に,幾つかの元を付け足すことで,
に,幾つかの元を付け足すことで,  を含む体
を含む体  を作れるとき,
を作れるとき,  を
を  の 拡大体 (もしくは単に 拡大 )と呼びます.
の 拡大体 (もしくは単に 拡大 )と呼びます.
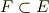
群論では,群の部分群を考えることに興味があり,正規部分群,中心,固定部分群など,部分群に関する色々な話題がありました.一方,体論で興味があるのは,ある体に何か元をつけたして体を拡大していくことです.
さて,体  の元を
の元を 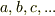 とし,ここに新たに元
とし,ここに新たに元  を添加する場合を考えてみましょう.体は演算に関して閉じていますから,もともと
を添加する場合を考えてみましょう.体は演算に関して閉じていますから,もともと  に含まれていた元と
に含まれていた元と  を四則演算して組み合わせた元,例えば
を四則演算して組み合わせた元,例えば 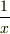 なども
なども  に含まれるなければなりません.そのため,元を一個だけ添加したつもりでも,通常,拡大体は
に含まれるなければなりません.そのため,元を一個だけ添加したつもりでも,通常,拡大体は 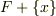 よりずっと大きな集合になることに注意してください.
よりずっと大きな集合になることに注意してください.

いま,添加された元と,それらの四則演算によって新しく増えた元をまとめて 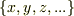 と書きましょう.つまり
と書きましょう.つまり  です.
です.  が
が  や
や  を含むことを考えれば,一般に
を含むことを考えれば,一般に  の元は全て
の元は全て 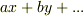 のように,
のように,  の元と新たに増えた元の線形結合の形で表現できるはずです.また,
の元と新たに増えた元の線形結合の形で表現できるはずです.また,  の元と
の元と  の元の間には分配法則
の元の間には分配法則 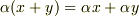 がなりたちます.これより,『
がなりたちます.これより,『  は
は  上のベクトル空間になっている』と見ることできます.
上のベクトル空間になっている』と見ることできます.
Important
体  の拡大体
の拡大体  は,
は,  上のベクトル空間になっています.
上のベクトル空間になっています.
ベクトル空間の基底は新たに増えた元 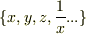 で,係数は
で,係数は  の元
の元  というわけです.また,
というわけです.また,  上のベクトル空間と見たときの
上のベクトル空間と見たときの  の次元を EのF上の次数 もしくは 拡大次数 と呼び,
の次元を EのF上の次数 もしくは 拡大次数 と呼び, ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) と書きます.
と書きます. ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) が有限のとき
が有限のとき  を 有限次拡大体 ,無限のとき 無限次拡大体 と呼びます.
を 有限次拡大体 ,無限のとき 無限次拡大体 と呼びます.
拡大体の具体的な例は,次のセクションで見ていきます.
拡大体の拡大次数
ここで,拡大体の表記法を紹介しておきます.体  に新たに代数的な元
に新たに代数的な元 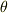 を添加して拡大体を作るとき,その拡大体を
を添加して拡大体を作るとき,その拡大体を 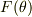 のように書きます.特に,元を一個だけ添加して得られる拡大体を 単純拡大体 と呼びます.
のように書きます.特に,元を一個だけ添加して得られる拡大体を 単純拡大体 と呼びます. 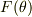 は,
は,  に
に 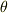 だけ添加した拡大体ですので,単純拡大体です.
だけ添加した拡大体ですので,単純拡大体です.
| [*] | 拡大体の元について,再び例とともに注意を喚起しておきます. 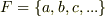 に に  を添加した拡大体を考えます. を添加した拡大体を考えます.  が が  ならば, ならば,  の形の数を四則演算しても,やはり の形の数を四則演算しても,やはり  の形のままですので, の形のままですので,  の元は全て の元は全て  の形に書けると言えます.( の形に書けると言えます.( 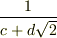 の形のものも,分母・分子に の形のものも,分母・分子に 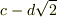 を掛けて整理すれば,全て を掛けて整理すれば,全て  の形に帰着します.)これより, の形に帰着します.)これより, 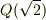 の拡大次数は の拡大次数は 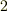 です.一方,もし です.一方,もし 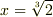 なら, なら,  の二乗 の二乗 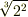 という元も新たに出てきてしまいますので, という元も新たに出てきてしまいますので,  の元は一般に の元は一般に  のように表わされることになり, のように表わされることになり, 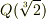 の拡大次数は の拡大次数は 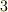 になります.このように,累乗根を添加するときには拡大次数に注意が必要です.また,代数的元ではありませんが, になります.このように,累乗根を添加するときには拡大次数に注意が必要です.また,代数的元ではありませんが, 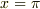 の場合を考えてみましょう. の場合を考えてみましょう.  を累乗していっても有理数になることはありませんし, を累乗していっても有理数になることはありませんし,  というような元も分母・分子を払うというような操作によってはこれ以上整理できません.つまり というような元も分母・分子を払うというような操作によってはこれ以上整理できません.つまり  を四則演算することで,新しい元は無限に出てきてしまうわけで, を四則演算することで,新しい元は無限に出てきてしまうわけで, 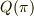 は無限次拡大体になります.(ただし,ここの議論は は無限次拡大体になります.(ただし,ここの議論は  を繰り返し四則演算していっても有理数になることはない,という事実を前提にしました.)添加する元が一個だけでも,どんな元を添加するかによって拡大次数は様々です.重要なのは,どんな元を添加するかです. を繰り返し四則演算していっても有理数になることはない,という事実を前提にしました.)添加する元が一個だけでも,どんな元を添加するかによって拡大次数は様々です.重要なのは,どんな元を添加するかです. |
添加した元 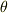 が, もとの体上で何次方程式の解になっていたかを考えても拡大次数が分かります.
が, もとの体上で何次方程式の解になっていたかを考えても拡大次数が分かります.  は二次方程式の解ですから,拡大次数は
は二次方程式の解ですから,拡大次数は 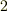 です.この辺りの事情は 最小分解体と代数的閉体 で明らかにする予定です.
です.この辺りの事情は 最小分解体と代数的閉体 で明らかにする予定です.
例
複素数体は,実数体の拡大体で,拡大次数は 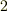 であることを確認してみてください.
であることを確認してみてください.
練習問題
有理数体 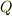 に,
に, 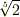 を添加してできる拡大体を考えます.
を添加してできる拡大体を考えます.
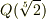 の元が一般にどのような形をしているかを示して下さい.
の元が一般にどのような形をしているかを示して下さい.- 拡大次数が
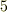 であることを確認してください.
であることを確認してください. 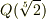 を
を  上のベクトル空間とみるとき,基底の組を一つ挙げて見てください.
上のベクトル空間とみるとき,基底の組を一つ挙げて見てください.
素体
逆に,部分体を考えて行くとき,これ以上小さな部分体が取れない(部分体は体自身のみ)となる体を 素体 と呼びます.有理数体は素体です.
theorem
有理数体 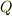 は素体です.
は素体です.
proof
仮に 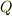 が部分体
が部分体 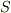 を持つとします.
を持つとします. 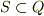 .
. 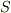 は体ですので,乗法の単位元
は体ですので,乗法の単位元 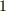 を含みます.加法の逆元も含むはずですので,
を含みます.加法の逆元も含むはずですので, 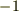 も
も 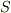 の元です.すると,全ての整数は
の元です.すると,全ての整数は 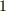 と
と 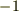 の加減で表わせてしまいますので,整数は全て
の加減で表わせてしまいますので,整数は全て 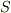 の元です.有理数は二つの整数
の元です.有理数は二つの整数 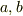 によって
によって 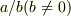 の形で表わされるはずですが,整数は全て
の形で表わされるはずですが,整数は全て 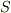 の元であり,また
の元であり,また 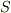 は乗法と(その逆演算である)除法についても閉じているはずですから,全ての有理数を含みます.よって
は乗法と(その逆演算である)除法についても閉じているはずですから,全ての有理数を含みます.よって  です.■
です.■
同様に,素数 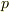 に関する整数の剰余体
に関する整数の剰余体 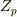 も素体になります.証明は,
も素体になります.証明は, 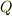 と同じようにして示せます.
と同じようにして示せます.
theorem
素数 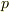 の剰余体
の剰余体 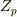 は素体です.
は素体です.
実は『全ての素体は, 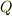 か
か 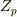 と同型である』と言えるのです.後ほど 素体 の記事で証明します.
と同型である』と言えるのです.後ほど 素体 の記事で証明します.
次数の定理
体  の拡大体を
の拡大体を  ,
,  の拡大体をさらに
の拡大体をさらに  とします.つまり,
とします.つまり,  は
は  と
と  の中間体です.
の中間体です.
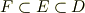
このとき,次数に関して次の定理が成り立ちます.とても重要な定理です.証明は,無限次拡大と有限次拡大の組み合わせを 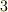 つに場合分けして示します.証明自体は簡単ですが,少し長く,あまり面白くないのでので,最初は結果だけを了承して先へ進んでも構いません.
つに場合分けして示します.証明自体は簡単ですが,少し長く,あまり面白くないのでので,最初は結果だけを了承して先へ進んでも構いません.
theorem
![[D:F]=[D:E][E:F]](./c614517755ba0bd951f6720c3f0ba28f.png)
proof
まず ![[D:E]=\infty](./e913b8f9e785f0a550f7ee07041b2a98.png) の場合を示します.つまり
の場合を示します.つまり  は
は  の無限次拡大になっています.このとき,
の無限次拡大になっています.このとき,  には
には  上線形独立な元
上線形独立な元 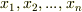 を何個でも含むことが出来ます(無限次拡大なので,線形独立な元は無限個あります).
を何個でも含むことが出来ます(無限次拡大なので,線形独立な元は無限個あります).  は
は  の部分体なので,
の部分体なので,  上線形独立な
上線形独立な 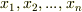 は,
は,  上でもやはり線形独立でなければなりません.これより
上でもやはり線形独立でなければなりません.これより ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) の次数に関わらず
の次数に関わらず ![[D:F]=\infty](./df31c1c15f5a9b11ac5d8dbb553965d4.png) となることが要請されます.(
となることが要請されます.( 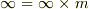 の場合の証明.)■
の場合の証明.)■
proof
次に ![[E:F]=\infty](./deea8651d30495eb83a6532e0d0900ea.png) の場合,
の場合,  には
には  上線形独立な元
上線形独立な元 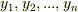 を何個でも含むことが出来ます.
を何個でも含むことが出来ます.  は
は  の拡大体なので,当然
の拡大体なので,当然 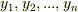 も含みます.これより
も含みます.これより ![[D:F]=\infty](./df31c1c15f5a9b11ac5d8dbb553965d4.png) が要請されます.(
が要請されます.( 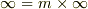 の場合の証明.)■
の場合の証明.)■
上の二つの場合に 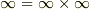 の場合を含めることが出来ます.最後に
の場合を含めることが出来ます.最後に ![[E:F]](./8595ba70325b37f8f3b5c90cda4e5059.png) も
も ![[D:F]](./a3eb8c0d8bd329e6bb35254d6f240cb4.png) も有限次拡大の場合の証明を示します.
も有限次拡大の場合の証明を示します.
proof
まず ![[D:E]=m, \ [E:F]=n](./0791911da16e9464358ffc1daebb96cf.png) と置きます.このとき
と置きます.このとき  は
は  上
上  次のベクトル空間,
次のベクトル空間,  は
は  上
上 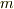 次のベクトル空間と見なせます.
次のベクトル空間と見なせます.  の任意の元は高々
の任意の元は高々 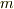 個の元の線形結合で表され,その個々の係数は,
個の元の線形結合で表され,その個々の係数は,  の元を係数とした高々
の元を係数とした高々  項の線形結合で表現されますから,
項の線形結合で表現されますから,  は
は  上
上 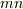 次のベクトル空間になっています.■
次のベクトル空間になっています.■
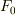 から次々に拡大体を重ねていくと,次のような拡大体の列が出来ます.
から次々に拡大体を重ねていくと,次のような拡大体の列が出来ます.