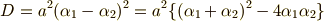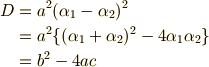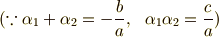代数方程式の判別式
代数方程式が与えられたとき,異なる実数解を持つのか,重解を持つのか,それとも異なる虚数解を持つのかを判別する式を代数方程式の判別式と呼びます.実際に方程式を解く前に判別式を考え,解に関する情報を得るのは大事なことです.
判別式の定義
次のような  次の代数方程式を考えましょう.
次の代数方程式を考えましょう.
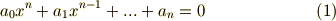
この方程式が  個の解(重解を含んでいても良い)
個の解(重解を含んでいても良い) 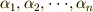 を持つとき,次のように,解の差を全ての組み合わせに関して掛け合わせたものを
を持つとき,次のように,解の差を全ての組み合わせに関して掛け合わせたものを 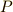 と置きます.
と置きます.
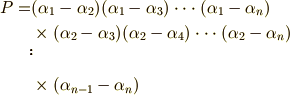
もしも式(1)が重解を持つとすれば, 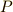 に含まれる括弧のうち,どれかが零になり,
に含まれる括弧のうち,どれかが零になり, 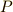 は零になるはずです.逆に,
は零になるはずです.逆に, 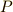 が零でないのは,式(1)の持つ全ての解が異なる場合だけだと言えます.
が零でないのは,式(1)の持つ全ての解が異なる場合だけだと言えます.
次に式(1)が重解を持たない場合に 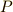 の二乗を考えてみましょう.実数を二乗すれば常に正になるはずですから,解が全て実数ならば
の二乗を考えてみましょう.実数を二乗すれば常に正になるはずですから,解が全て実数ならば 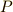 の二乗は正になります.もし,
の二乗は正になります.もし, 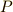 の二乗が負になれば,共役な虚数解が奇数組含まれているということになります.
の二乗が負になれば,共役な虚数解が奇数組含まれているということになります.
| [*] | 偶数組の共役虚数解(すなわち4の倍数個の虚数解)が含まれている場合には 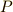 の二乗は正になります.すなわち,解が実数であることは の二乗は正になります.すなわち,解が実数であることは 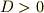 の十分条件であって,必要条件ではありません.一般に,判別式の符号だけから実数解か虚数解かを判別できるわけではないのです.二次方程式に限った話ならば, の十分条件であって,必要条件ではありません.一般に,判別式の符号だけから実数解か虚数解かを判別できるわけではないのです.二次方程式に限った話ならば, 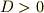 ならば方程式は実数解を, ならば方程式は実数解を, 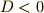 ならば虚数解を持つと判断できます. ならば虚数解を持つと判断できます. |
この 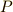 の二乗を用いて,次のように判別式
の二乗を用いて,次のように判別式 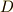 を定めます.係数
を定めます.係数 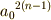 は,判別式が分数にならないよう,簡単化するために付けただけのもので,本質的な意味はありません.
は,判別式が分数にならないよう,簡単化するために付けただけのもので,本質的な意味はありません.
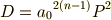
三次方程式の判別式
次に,三次方程式の判別式を考えます.
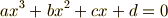
これが解 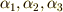 を持つとすると,判別式は定義より次式です.
を持つとすると,判別式は定義より次式です.
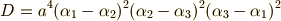
解と係数の関係を使って変形すれば,次式に至ります.途中の計算はやや面倒なので,ここでは省略します.時間とやる気のある人は,練習として確認してみてください.
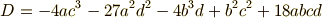

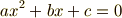
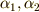 を持つとすると,判別式は定義より次式です.
を持つとすると,判別式は定義より次式です.