作図可能な正多角形

home > 代数学 >

このページのPDF版

サイトマップ

まず，作図可能数について次の定理がありました．一つの定理としてきちんと証明しませんでしたが，ギリシャ三大作図問題１，ギリシャ三大作図問題２，ギリシャ三大作図問題３の記事を通じて，次の定理の内容は既に示してあります．

theorem

作図可能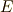体が有理数体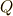の有限拡大である場合，拡大次数は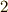の累乗になります． $[E:Q]=2^{r}$

次に，コンパスと定規だけで作図可能な正多角形を考えます．途中で上の定理を使います．また，１のｎ乗根の内容が前提となりますので，忘れてしまった人はもう一度復習しておいて下さい．

theorem

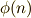正角形で，コンパスと定規だけで作図可能なのは $\phi (n)$ が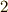の累乗のものに限ります．

proof

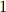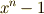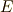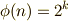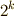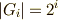正角形を作図することは，円周を個の円弧に分割することと同じです．さらに，複素平面上の単位円を個の円弧に分割することは，の乗根を求めること同じになります．よって，正角形が作図できる条件は， $x^{n}-1$ の最小分解体が作図可能体になることだと言えます．先ほどの定理より， $[E:Q]=\phi (n)=2^{k}$ が要請されます．逆に， $\phi (n)=2^{k}$ の場合，ガロア群 $\cal G \it (E/Q)=Z_{n}^{\times}$ の位数は $2^{k}$ となり，正規部分群の組成列として $\{ e\} =G_{0} \subset G_{1} \subset ... 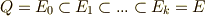\subset G_{k} = \cal G \it (E/Q)$ が考えられます．各部分群において， $|G_{i}|=2^{i}$ となっており，これは可解群です．これに対応しての部分体の昇鎖列を考えることが出来ます． $Q =E_{0} \subset E_{1} \subset ... \subset E_{k} =E$ ．隣り合った部分体はガロア拡大になっています．ガロア理論の基本定理によって，拡大次数について $[E_{i}:E_{i-1}]=[G_{k+1-i}:G_{G_{k-i}}]=2$ がなりたちます．（ガロア群と拡大体の包含関係は反変的であることに注意して下さい．）これより， [E:Q] は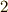の累乗になります． ■

作図可能な正多角形

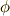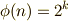いまの定理を使って，コンパスと定規で作図可能な正多角形を実際に考えてみましょう．オイラーの $\phi$ 関数について少し考えることになります．正角形が作図可能とすると，先ほどの定理より $\phi (n)=2^{k}$ と書けるはずです．

さて，私達はコンパスと定規だけで線分を二等分することは簡単にできますので，一つの正多角形が描けたら，その二倍の角数の正多角形を描くことは（労力は別として）簡単です．そこで，本質的に，奇数角形の正多角形に興味が向くことになります．さらに，奇数といっても，例えば 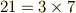$21=3\times 7$ 角形のような複合数の場合，正七角形が描けないのに，一足飛びに正二十一角形が描けるということは有り得ませんから（もし正二十一角形が描ければ，角を三つおきに結べば正七角形になるはずです），結局，正素数角形の作図可能性を調べることが本質的に重要だということになります．

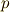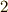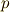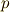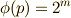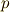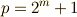いま，を素数とすると，〜 p-1 の数は全てと互いに素ですから， $\phi (p)=p-1$ です．一方，先ほどの結果より，正角形が作図可能なためには $\phi (p)=2^{m}$ と書けることが必要でした．これより，は $p=2^{m}+1$ を満たすことが要請されます．つまり，正素数角形で作図可能なのは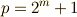， $p=2^{m}+1$ と表わせる素数に限るということです．

theorem

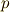を素数とすると，正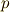角形が作図可能となるのは 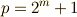$p=2^{m}+1$ と書ける場合に限ります．

ここに至り，正多角形の作図可能性を調べる問題は『 $2^{m}+1$ の形をした素数を探す』という問題に帰着しました． $2^{m}+1$ の形の数が素数となるのは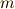，がどのような数の場合でしょうか？はじから順番に調べる手もありますが，次のような簡単な考察で，さらに形を絞り込むことができます．

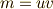もし，奇数を用いて m=uv と書けるとすると，次の因数分解がなりたちます．

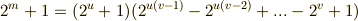
$2^{m}+1 = (2^{u}+1)(2^{u(v-1)}-2^{u(v-2)}+...-2^{v}+1)$

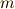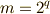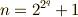これは $2^{m}+1$ が素数であるという前提に反しますので，はいかなる奇数でも割れない数でなければなりません．これより $m=2^{q}$ が要請されます．結局，正角形が作図可能可能となるのは， $n= 2^{2^{q}}+1$ の場合に限られるのです．

theorem

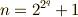正角形（は素数）が定規とコンパスで作図可能となるのは， $n= 2^{2^{q}}+1$ と書ける場合に限ります．

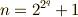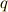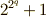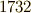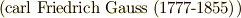ここで出てきた $n= 2^{2^{q}}+1$ の形で書ける素数を フェルマーの素数 と呼びます．フェルマー( $\text{Pierre de Fermat (1601-1665)}$ )が最初にこの形の素数を研究したそうです．少し計算してみれば分かりますが，が少し大きくなると猛烈に $2^{2^{q}}+1$ は大きくなりますから，手計算ではとても求められません．当初は，フェルマーの素数は無限個あるだろうと漠然と予想されていました．しかし， 1732 年，ガウス $(\text{carl Friedrich Gauss (1777-1855)})$ が次の式を示しました．たった一行の式で大方の予想を否定してしまったのですから，こういう因数分解を示す瞬間というのは，本当に気持ち良いものだと思います．

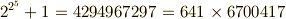
$2^{2^{5}}+1 =4294967297= 641 \times 6700417$

これによって 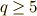$q \ge 5$ の場合は素数ではないことが示され，フェルマー素数には 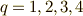q=1,2,3,4 の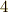つしか無いことが分かりました．

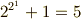
$2^{2^{1}}+1 = 5$

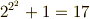
$2^{2^{2}}+1 = 17$

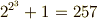
$2^{2^{3}}+1 = 257$

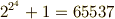
$2^{2^{4}}+1 = 65537$

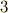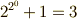作図可能な正素数角形は，三角形（は $2^{2^{0}}+1 = 3$ ですが，通常フェルマー素数には数えません）を加えて，この五種類しかないわけです．『正七角形を作図せよ』という問題が，古代ギリシャの作図問題の一つとして加える場合がありますが，正七角形の作図が不可能なことがこれで示されます．正五角形の作図法は，古代ギリシャで既に知られていましたが，正十七角形の作図法は 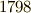1798 年にガウスが発見するまで知られていませんでした．当時，十九歳だったガウスは，朝ベッドで目を覚ますなり正十七角形の作図法が頭に浮かんだということです．また，自分の墓石にも正十七角形を刻むように遺言しました．（墓石の写真で見る限り正十七角形は刻まれていないようですが，一説には墓石屋が難しさのあまり断ったということです．実際，正十七角形はほとんど円のようになってしまうため，それと分かるように石に彫るのは至難の業でありましょう．その代わり，ガウスの生まれ故郷であるブラオンシュヴァイク市に現在立つガウス像は，正十七角形の台座に乗っているということです．写真では台座の形はよく分かりませんね．）

Braunschweig市にあるガウス像

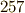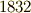正 257 角形は， 1832 年にリヒェロット 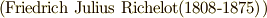$(\text{Friedrich Julius Richelot(1808-1875)})$ によって作図されました．こうなると，実際的にはほとんど円と変わりませんし，わずかな誤差で図がずれて来ますから，作図は大変な作業だったと思います．正 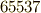65537 角形は，リンデン市でギムナジウムの教授をしていたヘルメス( $\text{Johann Hermann Gustav Hermes (1846-1912)}$ )により， 1894 年前後に作図されましたが，なんと，作図には年もかかったということです！恐ろしい執念です．この労作はゲッチンゲン大学図書館に収蔵されていますが，戦時中の空襲や洪水も奇跡的に免れ，今も現存しており，閲覧可能だということです．ゲッチンゲンへご旅行の際は，大学図書館にぜひ行ってみましょう．

[home] [代数学] [ページの先頭]