正五角形の作図
この記事では,正五角形の作図を考えてみたいと思います. 作図できる正多角形 の結果より,正五角形は定規とコンパスで作図できる正多角形だということが分かりましたが,既に作図方法を知っている人もいると思います.ここでは,初等幾何としてではなく,代数学的な視点から捉えなおしてみることに意味があると思います.
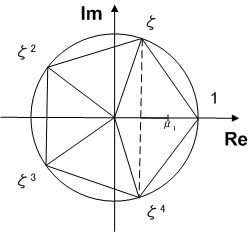
正五角形の作図は,円周を 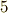 つに等分する問題と同じです.ここで,
つに等分する問題と同じです.ここで, 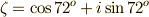 として,拡大体
として,拡大体 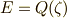 を考えます.
を考えます. 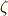 の最小多項式は次式で,
の最小多項式は次式で, 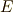 は
は 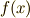 の最小分解体になっています.
の最小分解体になっています.
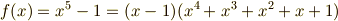
ここで 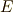 を
を 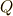 上のベクトル空間と見たとき,
上のベクトル空間と見たとき, 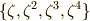 は基底を張っており,
は基底を張っており, 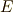 の元は一般に
の元は一般に 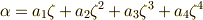 と書けます.(
と書けます.( 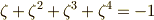 が成り立つことに注意. 1のn乗根 参照.)拡大次数は
が成り立つことに注意. 1のn乗根 参照.)拡大次数は ![[E:Q]=4](./8251d7d95787dc97df131ebe08f5c625.png) ですのでガロア群の位数は
ですのでガロア群の位数は  で,
で, 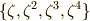 を置換する元からなります.これは,
を置換する元からなります.これは, 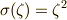 と置くと,
と置くと, 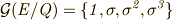 と表わされる巡回群です.
と表わされる巡回群です.
自明な部分群を除くと, 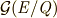 は正規部分群
は正規部分群 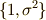 を持ちます.(正規真部分群はこれだけです.)そこで,ガロア理論の基本定理により,
を持ちます.(正規真部分群はこれだけです.)そこで,ガロア理論の基本定理により, 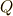 と
と 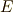 には中間体
には中間体 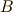 が存在し,
が存在し, 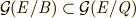 がなりたつことが予想されます.つまり,
がなりたつことが予想されます.つまり, 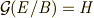 と表記すると,中間体
と表記すると,中間体 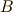 が群
が群 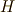 の固定体になっているというわけです.( ガロア理論の基本定理 参照.)
の固定体になっているというわけです.( ガロア理論の基本定理 参照.)
ここまでは,既に勉強したガロア理論の基本定理から予想されるカラクリを書き並べてみただけですが,ここまでの説明に引っかかるところある人は,この段階でよく頭を整理してみて下さい.大事なのは,ここまでの大筋で,ここから先は実際の計算です.
ガロア理論の計算
まず, 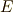 の元
の元 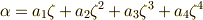 が
が 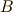 に含まれる条件は,
に含まれる条件は, 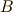 の元が
の元が 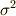 で動かされないことですから
で動かされないことですから 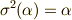 がなりたつことです.では,実際に計算して係数の条件を決めてみましょう.
がなりたつことです.では,実際に計算して係数の条件を決めてみましょう. 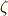 の指数が
の指数が 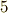 より大きくなると,
より大きくなると,  で
で 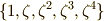 に戻ってくることに注意して下さい.途中の式変形は,添字の変化が分かりやすいように一行ずつ丁寧に書きました.
に戻ってくることに注意して下さい.途中の式変形は,添字の変化が分かりやすいように一行ずつ丁寧に書きました.
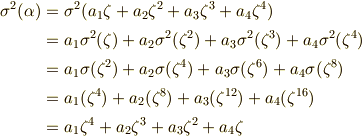
一行目と最終行を見比べて, 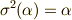 となるのは
となるのは 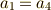 かつ
かつ 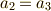 の場合であることが分かります.よって,
の場合であることが分かります.よって,  の元は一般に次のような形に書けることが分かります.(
の元は一般に次のような形に書けることが分かります.( 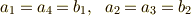 と置きました.)
と置きました.)
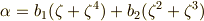
そこで,さらに 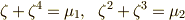 と置くと,次のような興味深い関係が見えてきます.
と置くと,次のような興味深い関係が見えてきます.
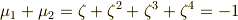
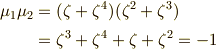
これを見てピンッと来て欲しいのですが, 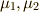 は解と係数の関係より,方程式
は解と係数の関係より,方程式 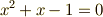 の解となっています!!
の解となっています!!
| [*] | 作図可能数について ギリシャ三大作図問題3 で触れましたが,作図可能数は有理数体 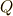 の の  次拡大体に限られました. 次拡大体に限られました. 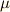 は二次方程式の解ですから, は二次方程式の解ですから, 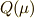 は は 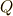 の二次拡大体であり,作図可能体だと言えるわけです.逆に言えば,仮に の二次拡大体であり,作図可能体だと言えるわけです.逆に言えば,仮に 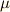 が三次方程式の解として与えられる数とすれば正五角形は作図不可能なわけで,二次方程式の解として が三次方程式の解として与えられる数とすれば正五角形は作図不可能なわけで,二次方程式の解として 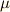 を得られたことが本質的に重要です.これが三次方程式だったら,もう作図不可能なわけで,勘のいい人は,作図可能と聞いた時点で,中間体が二次方程式の分解体になっていることが予想できることでしょう. を得られたことが本質的に重要です.これが三次方程式だったら,もう作図不可能なわけで,勘のいい人は,作図可能と聞いた時点で,中間体が二次方程式の分解体になっていることが予想できることでしょう. |
解の公式より, 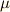 を求めることが出来ます.
を求めることが出来ます.
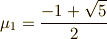

ただし, 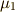 と
と 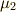 の符号は,
の符号は, 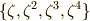 の図形的関係から決めました.
の図形的関係から決めました.
これより,より具体的に 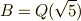 であることが分かりました.
であることが分かりました. 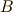 上の代数方程式を考えれば,
上の代数方程式を考えれば, 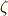 と
と  は
は 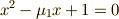 の解として,
の解として, 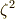 と
と 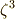 は
は 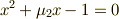 の解として与えられます.
の解として与えられます.
| [†] | なんだかガロア群や同型写像を色々考えましたが,結局求めたいのは 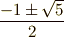 だったのです.これなら,三角関数の加法定理を使って だったのです.これなら,三角関数の加法定理を使って 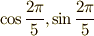 から,高校生でも求めることが出来る値です.しかし三角関数を使うのは代数的方法ではありません.(三角関数は超越関数ですね.)私達は純粋に代数的な方法として,最後に二次方程式に辿りつくような方法を考え,確かに から,高校生でも求めることが出来る値です.しかし三角関数を使うのは代数的方法ではありません.(三角関数は超越関数ですね.)私達は純粋に代数的な方法として,最後に二次方程式に辿りつくような方法を考え,確かに 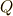 の二次拡大であるから作図可能である云々という点を確認しました.あくまで代数的にという点が,難しかったわけで,単になんでもいいから正五角形を作図することだけが目的なら,三角関数を使えば簡単な話だったのです.一番簡単なのは,正五角形をフリーハンドで適当に描き(!?),補助線を引いてピタゴラスの定理を使って の二次拡大であるから作図可能である云々という点を確認しました.あくまで代数的にという点が,難しかったわけで,単になんでもいいから正五角形を作図することだけが目的なら,三角関数を使えば簡単な話だったのです.一番簡単なのは,正五角形をフリーハンドで適当に描き(!?),補助線を引いてピタゴラスの定理を使って 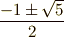 を求めてしまうことです.図形を描くために計算しているのに,最初に図形を描いてしまったのでは論理的に逆ですが,手段を選ばないというならそんな方法もあります.飽くまで,代数的な解放は一種の美的ゲームのようなものですから,今までの論理やガロア理論の美しさを楽しんでください. を求めてしまうことです.図形を描くために計算しているのに,最初に図形を描いてしまったのでは論理的に逆ですが,手段を選ばないというならそんな方法もあります.飽くまで,代数的な解放は一種の美的ゲームのようなものですから,今までの論理やガロア理論の美しさを楽しんでください. |
正五角形の作図法
ここからはおまけですが,いよいよ作図法を考えることにします.図より, 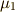 が作図できれば,
が作図できれば, 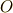 と
と 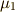 の中点から垂線を立て,頂点
の中点から垂線を立て,頂点 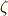 ,
,  が求まりますので正五角形が作図できることが分かります.
が求まりますので正五角形が作図できることが分かります. 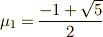 ですが,ピタゴラスの定理で
ですが,ピタゴラスの定理で 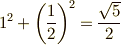 が成り立つことを使うと,意外と簡単に作図できます.以下に作図方法を解説しておきます.
が成り立つことを使うと,意外と簡単に作図できます.以下に作図方法を解説しておきます.

【正五角形の作図法】
- 縦横に二本の線を引き,交点を
 とします.
とします. 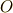 を中心に円を描きます.
を中心に円を描きます. - 円と直線の交点を,
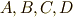 と名づけます.
と名づけます.  の中点に
の中点に 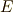 を取ります.
を取ります. - 線分
 の長さは
の長さは 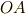 を
を 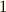 とすると
とすると 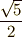 です.
です. 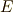 を中心に半径
を中心に半径  の円を描き
の円を描き 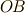 との交点を
との交点を 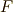 とします.
とします.- 線分
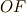 の長さは
の長さは 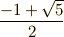 になっています.
になっています. 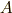 を中心に半径
を中心に半径 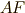 の円を描きます.最初の円との交点が正五角形の頂点になります.
の円を描きます.最初の円との交点が正五角形の頂点になります.