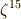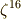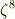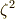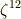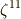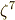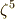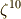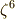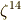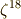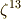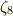正十七角形の作図
正十七角形の作図法がガウス  によって発見された話は非常に有名です.
によって発見された話は非常に有名です. 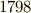 年
年 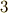 月
月 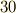 日,ガウスはベッドで目を醒ますなりこの作図法を思いついたということです.哲学者になろうか数学者になろうか迷っていたガウスは,この発見に自信を得て数学者の道を選んだという話もあります.(ガウスの父は,ガウスに煉瓦職人になって欲しいと思っていました!)
日,ガウスはベッドで目を醒ますなりこの作図法を思いついたということです.哲学者になろうか数学者になろうか迷っていたガウスは,この発見に自信を得て数学者の道を選んだという話もあります.(ガウスの父は,ガウスに煉瓦職人になって欲しいと思っていました!)
ガウスの作図法はガウスの著書 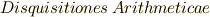 に出ていますが,同書でガウスは『定規とコンパスで作図できる正
に出ていますが,同書でガウスは『定規とコンパスで作図できる正 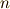 角形は,
角形は, 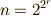 の場合に限る』ことも論じており,体論が完成する以前の議論としては秀逸なものです.もっとも,ガウスは自分の研究を公表しない癖があり,遺稿を検討したところでは,ガウスが既に抽象代数の群論や体論に極めて近い概念に到達していたらしいことも分かっています.きちんとアイデアを発表してくれていれば,数学の進歩はあと
の場合に限る』ことも論じており,体論が完成する以前の議論としては秀逸なものです.もっとも,ガウスは自分の研究を公表しない癖があり,遺稿を検討したところでは,ガウスが既に抽象代数の群論や体論に極めて近い概念に到達していたらしいことも分かっています.きちんとアイデアを発表してくれていれば,数学の進歩はあと 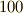 年以上早かったかも知れません.
年以上早かったかも知れません.

史上最大の数学者と言われるガウス.ガウスが手を出さなかった分野は少ないくらいだ.
正十七角形
基本的には 正五角形の作図 と全く同じ議論を使いますが,正十七角形の作図法はもっと複雑になります.議論の意味自体がよく分からない場合は, 正五角形の作図 に戻って復習してください.『作図可能である』という性質の一番のポイントは,途中の中間体が二次拡大(二次方程式の分離拡大体)になっていることです.このことを確認しながら読み進めて下さい.
まず, 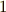 の
の 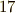 乗根を考えます.
乗根を考えます.
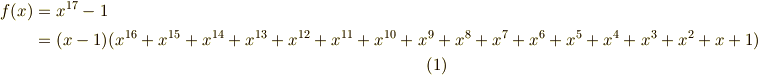
ここで, 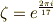 と置くと,
と置くと, 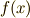 の解を
の解を  と表わすことが出来ます.また
と表わすことが出来ます.また 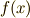 の最小分解体を
の最小分解体を 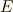 とすると,
とすると, 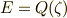 ,
, ![[E:Q]=16](./4148401fc17826279550d8cc10f28ab5.png) となり,
となり, 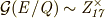 となるところまではもう大丈夫でしょう.
となるところまではもう大丈夫でしょう. 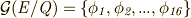 と置き,
と置き, 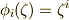 と考えると,
と考えると, 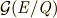 は
は 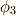 によって生成される巡回群になります.
によって生成される巡回群になります. 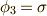 と置きましょう.一般に
と置きましょう.一般に 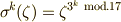 となります.
となります.
指数の 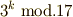 の部分を
の部分を 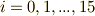 について表にしておきます.確かに重複がないことを確認してください.(
について表にしておきます.確かに重複がないことを確認してください.( 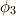 以外の元を選ぶと,こうはならないのです.なぜ
以外の元を選ぶと,こうはならないのです.なぜ 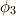 を生成元に選んだか?という点ですが,最高
を生成元に選んだか?という点ですが,最高 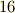 回試行錯誤してみれば分かることです.ここでは時間節約のため,いきなり結果を書きましたが,特に秘密の方法があるわけではなく,試行錯誤を重ねてみるしかありません.)
回試行錯誤してみれば分かることです.ここでは時間節約のため,いきなり結果を書きましたが,特に秘密の方法があるわけではなく,試行錯誤を重ねてみるしかありません.)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 9 | 10 | 13 | 5 | 15 | 11 | 16 | 14 | 8 | 7 | 4 | 12 | 2 | 6 |
この表を使えば,  を
を 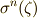 に一意的に置き換えること(その逆も)が出来ます.そこで,ガロア群の元を次のように置きなおすことにします.
に一意的に置き換えること(その逆も)が出来ます.そこで,ガロア群の元を次のように置きなおすことにします.
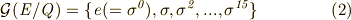
この表は後で何度も利用することになります.さて,次に考えることはガロア群の正規部分群です.これを見つけ出すには,正規部分群の位数が 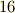 の約数になることを念頭に,上の表を使うことで,ある程度は勘が働きますが,基本的には色々試してみるほかありません.読者のみなさんと苦楽を共にしたいところでありますが,ここでは結果だけ書くことにさせて頂きます.
の約数になることを念頭に,上の表を使うことで,ある程度は勘が働きますが,基本的には色々試してみるほかありません.読者のみなさんと苦楽を共にしたいところでありますが,ここでは結果だけ書くことにさせて頂きます.
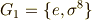
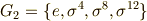

この三つが 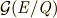 の(自明ではない)正規部分群で,位数はそれぞれ
の(自明ではない)正規部分群で,位数はそれぞれ 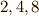 です.部分群の位数は
です.部分群の位数は 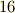 の約数になっていなければいけませんので,他には存在しません.部分群の列は次のようになります.
の約数になっていなければいけませんので,他には存在しません.部分群の列は次のようになります.
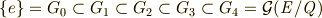
ガロア理論の基本定理により,これに対応して 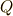 と
と 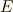 の間には次のように中間体
の間には次のように中間体 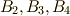 が存在することが言えます.ガロア群の部分群の組成列と,中間体の反変的な包含関係に,いま一度注意して下さい.(嗚呼,ガロア理論は美しいですね〜♪)
が存在することが言えます.ガロア群の部分群の組成列と,中間体の反変的な包含関係に,いま一度注意して下さい.(嗚呼,ガロア理論は美しいですね〜♪)

この後の方針は, 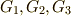 の元に対し,
の元に対し, 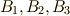 がそれぞれ固定体であることを使って
がそれぞれ固定体であることを使って 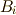 の元の形を割り出し,
の元の形を割り出し, 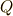 から
から 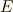 へ至る拡大体の系列をつぶさに調べます.各段階が二次拡大であれば,それぞれ二次方程式の解を添加することで得られる拡大体だというわけですから作図可能体です.( ギリシャ三大作図問題 参照.)もしどこかに三次拡大があれば,そこから先の拡大体は作図可能ではなくなりますが,ガウスが示したように正十七角形は作図可能なのですから,結果から先に言うと,各拡大は二次拡大になっています.以下,そのことを確認していきましょう.
へ至る拡大体の系列をつぶさに調べます.各段階が二次拡大であれば,それぞれ二次方程式の解を添加することで得られる拡大体だというわけですから作図可能体です.( ギリシャ三大作図問題 参照.)もしどこかに三次拡大があれば,そこから先の拡大体は作図可能ではなくなりますが,ガウスが示したように正十七角形は作図可能なのですから,結果から先に言うと,各拡大は二次拡大になっています.以下,そのことを確認していきましょう.
B3
まず  を固定体とする
を固定体とする 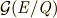 の部分群
の部分群 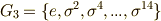 は
は 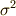 によって生成される巡回群ですから,
によって生成される巡回群ですから, 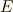 の元
の元 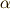 が
が  に含まれるかどうかは
に含まれるかどうかは 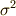 による写像だけを調べればよく,
による写像だけを調べればよく, 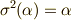 が必要十分条件となります.
が必要十分条件となります.
ここで 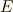 の元の基底ですが,
の元の基底ですが,  を簡単のため
を簡単のため 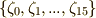 と書くことにします.このように書くと,
と書くことにします.このように書くと, 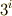 を書く手間が省けるだけでなく,
を書く手間が省けるだけでなく, 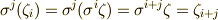 のような添字の関係がなりたち,写像の計算が大変便利です.
のような添字の関係がなりたち,写像の計算が大変便利です.
一般に, 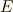 の元を
の元を 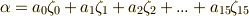 と置きましょう.この
と置きましょう.この 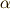 の
の 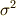 による写像を考えます.(
による写像を考えます.( 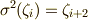 に注意しましょう.)
に注意しましょう.)
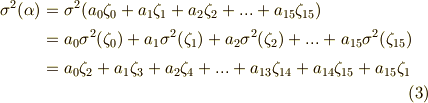
これより, 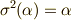 が成り立つためには,次の二つの条件が必要だと分かります.
が成り立つためには,次の二つの条件が必要だと分かります.

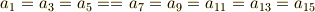
よって, 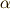 を次のように書き直すことが出来ます.
を次のように書き直すことが出来ます.
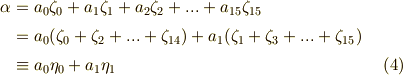
ここで置いた 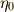 と
と 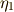 は,それぞれ
は,それぞれ 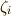 の
の 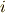 が偶数のものと奇数のものを足し合わせたものです.
が偶数のものと奇数のものを足し合わせたものです.
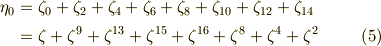
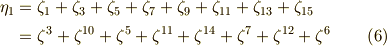
当然, 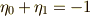 がなりたちます.次に,積
がなりたちます.次に,積  を考えてみましょう.式を展開するのは見にくいので,式
を考えてみましょう.式を展開するのは見にくいので,式 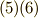 の項の乗積表を作って考えた方が見やすいでしょう.計算はかなり面倒ですが,
の項の乗積表を作って考えた方が見やすいでしょう.計算はかなり面倒ですが, 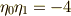 が分かります.
が分かります.
表より, 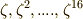 がそれぞれ
がそれぞれ 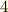 回ずつ出てきていますので,
回ずつ出てきていますので, 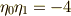 が分かります.
が分かります.
| [*] | 実際に式 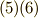 を地道に計算しなくても, を地道に計算しなくても, 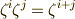 の形の項の項数が の形の項の項数が 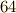 個であること,全ての組み合わせを網羅するように添字が出てくるはずであることを考えれば,ここには 個であること,全ての組み合わせを網羅するように添字が出てくるはずであることを考えれば,ここには 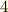 組の 組の  が含まれており, が含まれており, 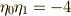 となることが予想されます.また, となることが予想されます.また,  は は 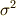 に対して不動なので に対して不動なので  の元であり,さらに の元であり,さらに 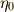 と と 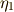 に関して対称なため, に関して対称なため, 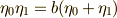 の形に書けることもすぐに分かります.このような考えを利用すると,実際に の形に書けることもすぐに分かります.このような考えを利用すると,実際に  を全て展開して計算しなくても を全て展開して計算しなくても 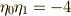 がすぐに分かったりします. がすぐに分かったりします. |
もう一度, 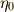 と
と 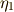 の関係式をまとめてみましょう.
の関係式をまとめてみましょう.


式 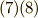 と二次方程式の解と係数の関係より,
と二次方程式の解と係数の関係より, 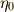 と
と 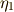 は
は 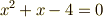 の解であることが分かります.
の解であることが分かります.
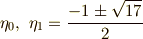
中間体  は
は 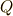 の二次拡大体で,
の二次拡大体で,  が分かりました.二次拡大体ですから,もちろん
が分かりました.二次拡大体ですから,もちろん  は作図可能体です.
は作図可能体です.
| [†] | これが三次拡大以上ならば,一般に  は作図可能体にならないわけで,逆に言えば,ここが上手く二次拡大になるので正十七角形は作図可能なわけです.引き続き, は作図可能体にならないわけで,逆に言えば,ここが上手く二次拡大になるので正十七角形は作図可能なわけです.引き続き,  も も  の二次拡大, の二次拡大, 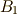 も も  の二次拡大になっていることが予想されます.まずは, の二次拡大になっていることが予想されます.まずは,  が二次拡大であったことを喜びましょう^^ が二次拡大であったことを喜びましょう^^ |
B2
次に,中間体  を考えます.
を考えます.  を固定体とする
を固定体とする 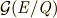 の部分群は
の部分群は 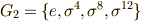 です.
です. 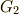 は
は 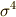 によって生成される巡回群なので,
によって生成される巡回群なので, 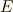 の一般の元
の一般の元 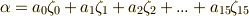 に対し,
に対し, 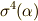 を考えると,
を考えると, 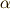 が
が  の元である必要十分条件は
の元である必要十分条件は 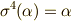 となることです.(
となることです.(  で行った手順と全く同じです.)
で行った手順と全く同じです.)
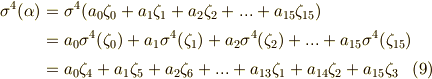
式 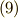 と
と 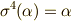 より,次の条件が要請されます.
より,次の条件が要請されます.
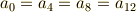
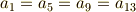
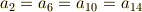
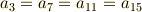
これより,一般に  の元は
の元は 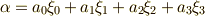 と書けることが分かります.ただし,
と書けることが分かります.ただし, 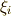 は次のように定義しました.
は次のように定義しました.
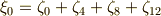
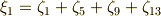
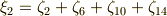
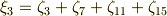
ここで, 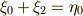 がなりたっています.また,次式に注意しましょう.
がなりたっています.また,次式に注意しましょう.
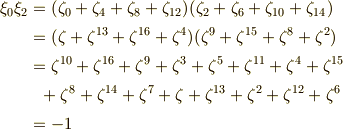
同様に,  ,
, 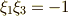 も言えます.これより,
も言えます.これより, 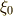 と
と 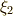 は
は 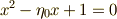 の解,
の解, 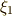 と
と 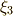 は
は 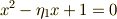 の解であることが分かります.(やはり二次方程式に帰着しましたね♪)
の解であることが分かります.(やはり二次方程式に帰着しましたね♪)
二つの二次方程式を 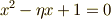 とまとめ,その解を
とまとめ,その解を 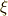 と置くと,
と置くと,  と表わせて,
と表わせて,  は
は  の二次拡大であり,やはり作図可能体であることが分かります.
の二次拡大であり,やはり作図可能体であることが分かります.
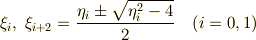
B1
引き続き,中間体 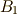 について調べます.手順は
について調べます.手順は  ,
,  の場合と全く同じですから,少しスピードアップして解説します.
の場合と全く同じですから,少しスピードアップして解説します. 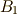 に対応する
に対応する 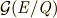 の部分群は
の部分群は 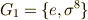 で,
で, 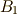 の元の係数には次の条件が必要となります.
の元の係数には次の条件が必要となります.
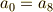
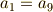
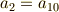
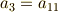

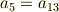
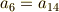
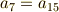
そこで,一般に 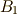 の元は
の元は 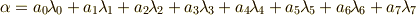 と書けます.ただし,ここで
と書けます.ただし,ここで 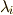 は次のように置きました.
は次のように置きました.
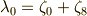
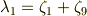
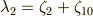
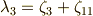
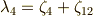
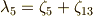

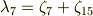
これら 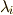 の和に関しては,次の関係がなりたっていることがすぐに分かります.
の和に関しては,次の関係がなりたっていることがすぐに分かります.
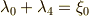
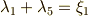
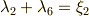
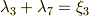
また,積は少し面倒ですので 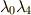 だけを例として示します.
だけを例として示します.
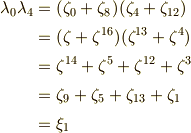
同様に, 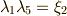 ,
, 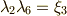 ,
, 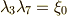 が示せます.結果として,
が示せます.結果として, 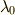 と
と 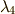 は
は 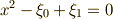 の解,
の解,  と
と 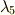 は
は 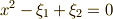 の解,
の解, 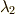 と
と 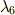 は
は 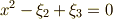 の解,
の解,  と
と 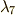 は
は 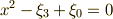 の解であることが分かりました.
の解であることが分かりました.
この 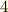 つの二次方程式の係数には
つの二次方程式の係数には 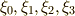 が入り混じっています.このままでも良いのですが,
が入り混じっています.このままでも良いのですが, 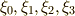 には次のような関係がなりたちますので,これを使うと添字を揃えることが出来ます.(この関係式は実際に計算して確認してみて下さい.)
には次のような関係がなりたちますので,これを使うと添字を揃えることが出来ます.(この関係式は実際に計算して確認してみて下さい.)
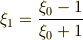
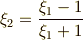
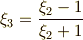
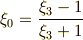
これらの関係式を使うと, 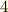 つずつまとめて『
つずつまとめて『  と
と 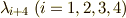 は,
は, 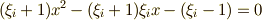 の解である』と表現することが出来ます.
の解である』と表現することが出来ます. 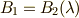 も二次拡大です.
も二次拡大です.
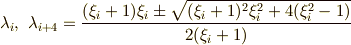
E
最後に 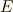 そのものを考えます.
そのものを考えます. 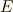 に対応するガロア部分群は
に対応するガロア部分群は 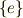 で,
で,  は
は 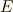 の元すべてを不動に保ちます.
の元すべてを不動に保ちます. 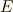 の元は一般に
の元は一般に 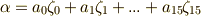 のように書けますが,
のように書けますが, 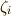 が満たすべき
が満たすべき 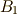 上の方程式は,
上の方程式は, 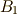 の議論で考えた
の議論で考えた 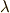 の定義式より簡単に求まります.まず,
の定義式より簡単に求まります.まず, 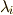 は次のように定義されました(再掲).
は次のように定義されました(再掲).
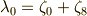
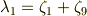
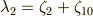
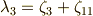
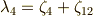
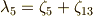

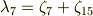
これと,次の関係に注意します.
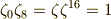
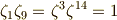
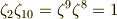
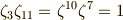
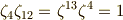

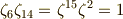
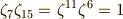
これより,  は,
は, 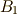 上の二次方程式
上の二次方程式  の解だと言えます.
の解だと言えます.  で,これも二次拡大であることが確認できました.
で,これも二次拡大であることが確認できました.
まとめ
いままでの結果をまとめて見ます.
 で,
で, 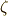 は
は 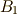 上の二次方程式
上の二次方程式 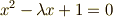 の解です.
の解です.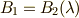 で,
で, 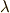 は
は  上の二次方程式
上の二次方程式  の解です.
の解です. で,
で, 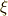 は
は  上の二次方程式
上の二次方程式 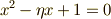 の解です.
の解です.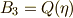 で,
で,  は
は 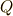 上の二次方程式
上の二次方程式 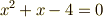 の解です.
の解です.
正十七角形が作図可能である理由は,この 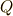 から
から 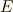 に至る 拡大体の列が全て二次拡大になっているから です.(作図可能体は,全て
に至る 拡大体の列が全て二次拡大になっているから です.(作図可能体は,全て 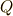 の
の 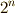 次拡大体として表現されるのでした. ギリシャ三大作図問題 を参照.)
次拡大体として表現されるのでした. ギリシャ三大作図問題 を参照.)
| [‡] | 次に作図可能な正素数角形は,正 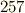 角形と正 角形と正 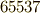 角形でした.これらの正多角形の頂点も 角形でした.これらの正多角形の頂点も 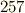 次円周等分方程式, 次円周等分方程式, 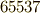 次円周等分方程式の解として与えられ,それぞれ 次円周等分方程式の解として与えられ,それぞれ 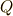 の の  次拡大体, 次拡大体, 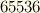 次拡大体に含まれる数が頂点を与えるわけですが,これらもやはり中間体を全て書き出せば,それぞれ隣り合う中間体とは二次拡大の関係になっているはずなのです.とても実際に普通の人間が出来る計算ではありませんが,ガロア理論を通して見る拡大体の構造の美しさが鑑賞できます. 次拡大体に含まれる数が頂点を与えるわけですが,これらもやはり中間体を全て書き出せば,それぞれ隣り合う中間体とは二次拡大の関係になっているはずなのです.とても実際に普通の人間が出来る計算ではありませんが,ガロア理論を通して見る拡大体の構造の美しさが鑑賞できます. |
実際に先ほどの二次方程式に対して解の公式を繰り返すことで, 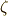 の値を求めてみましょう.
の値を求めてみましょう.
![\cos \left( \frac{2\pi }{17} \right) &= \Re [\zeta ] \\&=\Re[ \zeta_{0} ] \\&=\Re \left[ \frac{\lambda_{0} + \sqrt{\lambda_{0}^{2}-4}}{2} \right] \\&= \frac{\lambda_{0}}{2} \\&= \frac{1}{2}\cdot \frac{(\xi +1)\xi + \sqrt{(\xi +1)^{2}\xi^{2}+4(\xi^{2}-1)}}{2(\xi +1)} \\ &= \frac{1}{2}\cdot \frac{(\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) +1)\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) + \sqrt{(\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) +1)^{2}\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) ^{2}+4(\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) ^{2}-1)}}{2(\left( \frac{\eta + \sqrt{\eta^{2}-4}}{2} \right) +1)} \\ &= \frac{1}{2}\cdot \frac{(\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) +1)\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) + \sqrt{(\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) +1)^{2}\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) ^{2}+4(\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) ^{2}-1)}}{2(\left( \frac{\left( \frac{-1+\sqrt{17}}{2} \right) + \sqrt{\left( \frac{-1+\sqrt{17}}{2} \right) ^{2}-4}}{2} \right) +1)}](./f3a6e9b6173b0fce6abdfb49a383442d.png)
どんどん入れ子構造になっていきますが,整理すると次のようになります.  が作図可能数であることを眺めて味わって下さい.
が作図可能数であることを眺めて味わって下さい.
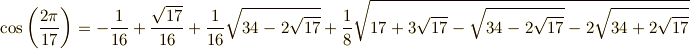
| [§] | しつこくも強調しておきますが,最初から三角関数の加法定理を使っていいのなら,  を求めること自体は大して難しい計算ではありません.しかし,三角関数は超越関数ですから,これでは代数的方法とは言えません.あくまで,代数的に,二次方程式を解くことを繰り返し,最後に を求めること自体は大して難しい計算ではありません.しかし,三角関数は超越関数ですから,これでは代数的方法とは言えません.あくまで,代数的に,二次方程式を解くことを繰り返し,最後に  を表現できた,というのが嬉しい点なのです. を表現できた,というのが嬉しい点なのです. |

ここから先は,相当マニアックな人向けです.
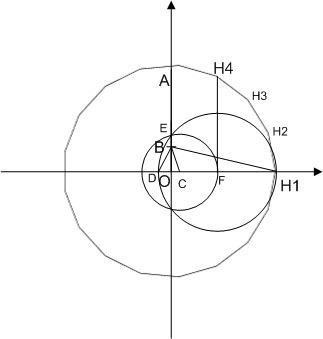
【正十七角形の作図法】
- まず適当に点
 と
と  を決め,円を描きます.
を決め,円を描きます.  に垂直な線を
に垂直な線を 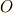 から引き,円との交点を
から引き,円との交点を  とします.
とします. の四分の一の点を
の四分の一の点を 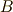 とします.
とします.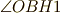 を四等分する点を
を四等分する点を 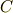 とします.
とします.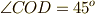 となる点
となる点  を取ります.
を取ります.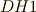 を直径とする円を描き,この円と
を直径とする円を描き,この円と  の交点を
の交点を  とします.
とします.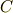 を中心に
を中心に 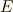 を通る円を描き,この円と
を通る円を描き,この円と 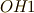 の交点を
の交点を 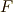 とします.
とします.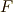 から
から 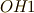 に垂直な線を引き,円との交点を
に垂直な線を引き,円との交点を 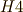 とします.
とします.- この
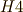 が
が 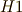 から見て
から見て 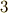 つ目の頂点になります.
つ目の頂点になります. 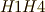 の長さで円弧を分割していくと,円を三周しながら
の長さで円弧を分割していくと,円を三周しながら  の順に頂点を定めることが出来ます.
の順に頂点を定めることが出来ます.