代数方程式を代数的に解く試み
『方程式を解く』という問題は,数学史でも,最も古い問題のひとつです.紀元前の古代バビロニア,エジプト,インドなどでは,すでに二次方程式が考えられていたそうです.もちろん,文字や記号を使って一般の数式を書く方法は未発達ですし,未知数というような概念もきちんとしていなかったため,古代の数学では,普通の文章を使って,特定の例題の解を示すという形で方程式を考えました.
実数解を持つ二次方程式の解の公式は古くから分かっていたようですが,三次方程式は簡単には解けませんでした.三次方程式の解の公式に関するドラマチックな歴史は, 三次方程式の解の公式 を参照して下さい.
| [*] | 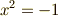 のような二次方程式を解く試みから,虚数 のような二次方程式を解く試みから,虚数 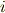 が発見されたとする説明がありますが,これは歴史的には正しくありません. が発見されたとする説明がありますが,これは歴史的には正しくありません. 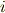 の発見は,三次方程式の解の公式に端を発します.詳しくは 複素平面 を参照ください. の発見は,三次方程式の解の公式に端を発します.詳しくは 複素平面 を参照ください. |
| [†] | 古代の方程式論では,一次の項は『長さ』,二次の項は『面積』,三次の項は『体積』に対応させ,幾何学的に式の意味を考えることがよく行われていました.最初に方程式を解く必要性に迫られた人は,恐らく,土地の分割や,穀物の計量といった実用的な意図を持っていたでしょうから,こうした対応はごく自然なことです.数学が驚異的に発展した古代ギリシャでは代数学は軽視され,幾何学が極端に重視されたため,古代ギリシャ人も方程式を幾何学的に考えていました.(例えば 平方完成の図形的イメージ 参照.)それでも,有名な デロス島の問題 のように,三次方程式は早くから知られていました. |
カルダノ(  ),フォンタナ(
),フォンタナ(  ),フェラーリ(
),フェラーリ(  )等により,三次方程式と四次方程式の解の公式が示されたあと,当然の流れとして,数学者は五次方程式の解の公式を探し始めました.三次方程式でさえ,解の公式を見つけるのは相当難しかったので,五次方程式の解の公式が簡単に見つかるとは,誰も考えていませんでした.しかし,当初は解の公式の存在そのものに関しては,楽観的な見方が主流でした.
)等により,三次方程式と四次方程式の解の公式が示されたあと,当然の流れとして,数学者は五次方程式の解の公式を探し始めました.三次方程式でさえ,解の公式を見つけるのは相当難しかったので,五次方程式の解の公式が簡単に見つかるとは,誰も考えていませんでした.しかし,当初は解の公式の存在そのものに関しては,楽観的な見方が主流でした.
ラグランジェの仕事
カルダノ以降,大きな進展は無かった方程式論に,その後のガロア理論に続く大きな一歩を踏み出したのが,フランスの大数学者・ラグランジェ(  )です.ラグランジェは,方程式の解と,解を置換する操作との関連に目をつけました.(置換については 対称群 を参照してください.)例えば,三次方程式の解を
)です.ラグランジェは,方程式の解と,解を置換する操作との関連に目をつけました.(置換については 対称群 を参照してください.)例えば,三次方程式の解を 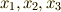 とし,
とし, 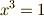 の解を
の解を 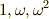 (ただし
(ただし 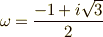 )とし,これを組み合わせて,次のような量を考えてみます.
)とし,これを組み合わせて,次のような量を考えてみます.
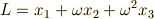
これを ラグランジェのリゾルベント と呼びます.  の並べ替えには
の並べ替えには 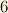 通りありますが,置換操作によって
通りありますが,置換操作によって 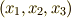 を入れ替えても,
を入れ替えても, 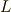 の取りうる値には二つしかありません.面白い!最初に,方程式の解と
の取りうる値には二つしかありません.面白い!最初に,方程式の解と 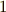 の
の 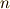 乗根を,こんな形で組み合わせてみよう,と考えたのは,ラグランジェの恐るべき慧眼で,ラグランジェは,ラグランジェのリゾルベントを用いて,五次以上の方程式の解を表現する方法も提案しています.
乗根を,こんな形で組み合わせてみよう,と考えたのは,ラグランジェの恐るべき慧眼で,ラグランジェは,ラグランジェのリゾルベントを用いて,五次以上の方程式の解を表現する方法も提案しています.
ラグランジェの解法は,改めて 累開冪拡大とガロア群の関係 で紹介しますので,ここでは詳しく説明しませんが,どうやら五次以上の方程式でも代数的に解ける場合というのは,解の入れ替えを 巡回置換 によって行える場合に限りそうだ,ということが分かってきました.(いま,チラッと 累開冪拡大とガロア群の関係 を見てもいいです.) 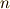 次方程式の可解性と,
次方程式の可解性と, 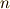 個の解の置換という,一見まったく関係なさそうな話題の関連性を見破ったという点において,ラグランジェの功績は画期的です.ただし,ラグランジェ自身は,五次以上の方程式にも解の公式があるだろうという楽観的な見方を最後まで持っており,せっかく置換操作を深く考えたにも拘らず,方程式の可解性そのものと巡回群の関係を追及するところまでには到らず,現代的な群論にまでは発展しませんでした
個の解の置換という,一見まったく関係なさそうな話題の関連性を見破ったという点において,ラグランジェの功績は画期的です.ただし,ラグランジェ自身は,五次以上の方程式にも解の公式があるだろうという楽観的な見方を最後まで持っており,せっかく置換操作を深く考えたにも拘らず,方程式の可解性そのものと巡回群の関係を追及するところまでには到らず,現代的な群論にまでは発展しませんでした

可解性と巡回群の関係に気づいたラグランジェ.群論まであと一歩だった.
| [‡] | ここで問題になっているのは,『方程式を代数的に解く』という話です.代数的に解くというのは,加減乗除と開冪( 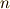 乗根を取る操作)だけを有限回使って,方程式の解を方程式の係数で表すということです.五次以上の方程式にも 代数学の基本定理 により,必ず複素数解まで考えれば解が存在しますし,代数的方法にこだわらなければ解を求めることは出来ます.例えば,無限回の操作を許せば解を表現することは出来ます.(現実的には,無限回の計算はどこか有限回で打ち切って近似になるわけですが,これはコンピューターを使った数値計算で方程式を解く際のアルゴリズムになります.)また,楕円関数を使って五次方程式の解を表現するというような方法もあります.数学者達が『代数的に解く』という方法にこだわったのは,一種のゲームだと考えられます.このゲームへ挑戦することで,実際的に五次方程式を解く云々というよりは,方程式の解とは何か,といったより本質的な問題への理解が発展し,現代代数学の基礎ができたのでした. 乗根を取る操作)だけを有限回使って,方程式の解を方程式の係数で表すということです.五次以上の方程式にも 代数学の基本定理 により,必ず複素数解まで考えれば解が存在しますし,代数的方法にこだわらなければ解を求めることは出来ます.例えば,無限回の操作を許せば解を表現することは出来ます.(現実的には,無限回の計算はどこか有限回で打ち切って近似になるわけですが,これはコンピューターを使った数値計算で方程式を解く際のアルゴリズムになります.)また,楕円関数を使って五次方程式の解を表現するというような方法もあります.数学者達が『代数的に解く』という方法にこだわったのは,一種のゲームだと考えられます.このゲームへ挑戦することで,実際的に五次方程式を解く云々というよりは,方程式の解とは何か,といったより本質的な問題への理解が発展し,現代代数学の基礎ができたのでした. |
ルッフィーニの仕事
ラグランジェの論文は 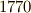 年に発表されましたが,これを発展させ,実質的に『五次方程式は一般には解の公式によって解けない』という結論に達したのは,医者でもあり数学者でもあった,イタリアのルッフィーニ(
年に発表されましたが,これを発展させ,実質的に『五次方程式は一般には解の公式によって解けない』という結論に達したのは,医者でもあり数学者でもあった,イタリアのルッフィーニ(  )です.この時代の多くの数学者や科学者と同じく,ルッフィーニもナポレオン戦争の影響を受け,大学の職を失ったりしていますが,あまり気にせず研究を続けました.
)です.この時代の多くの数学者や科学者と同じく,ルッフィーニもナポレオン戦争の影響を受け,大学の職を失ったりしていますが,あまり気にせず研究を続けました.
ルッフィーニの偉大な点は,『もしかして,五次方程式は代数的に解けないのではないか?』ということに気づいたことです.ルッフィーニ以前に五次方程式の問題に取り組んだ数学者は,オイラー  やラグランジェをはじめとして,ほぼ全員が『どんなに複雑でも,きっと解の公式はある』という希望を持っていました.こうした潮流の中で,
やラグランジェをはじめとして,ほぼ全員が『どんなに複雑でも,きっと解の公式はある』という希望を持っていました.こうした潮流の中で,  度逆の発想をするというのは,想像以上に勇気の要ることだったはずです.
度逆の発想をするというのは,想像以上に勇気の要ることだったはずです.
ルッフィーニは,ラグランジェの業績に触発され,それを発展させました.ラグランジェ自身は解を並べ替えるという操作を,群という考えに結びつけるには至りませんでしたが,ルッフィーニは現代の群論に近い考えを推し進め,巡回群,単純群などの概念を整理しました.ルッフィーニの用語法や書き方は,現代のものとは全然違っていますし,群論もまだ未発達でしたが,今風の言い方で書けば,ルッフィーニは次のような定理を考えたと言えます.
theorem
五次以上の対称群は,一般には可解群ではありません.
ルッフィーニの証明には小さな間違いが含まれていたようですが,これでルッフィーニを責めるのは酷に過ぎます.というのは,ルッフィーニはこの証明を 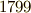 年に出版し,ラグランジェにも送りつけましたが(どうやら読んでないと感じ取ると,しつこく何度も送っています),当時の数学界からは無情なほどに無視され,ラグランジェもルッフィーニの証明を最後まで読まなかったようなのです.もし,誰か大物数学者が丁寧に証明を読めば,不備に気づいたかも知れませんし,指摘さえされれば,ルッフィーニは恐らく証明を改良できたでしょう.(実際,ルッフィーニ自身,
年に出版し,ラグランジェにも送りつけましたが(どうやら読んでないと感じ取ると,しつこく何度も送っています),当時の数学界からは無情なほどに無視され,ラグランジェもルッフィーニの証明を最後まで読まなかったようなのです.もし,誰か大物数学者が丁寧に証明を読めば,不備に気づいたかも知れませんし,指摘さえされれば,ルッフィーニは恐らく証明を改良できたでしょう.(実際,ルッフィーニ自身,  年,
年,  年,
年,  年,と何度も改良版を出版していますが,ほとんど無視されてしまいました.)
年,と何度も改良版を出版していますが,ほとんど無視されてしまいました.)

正当な評価を受けられず,気の毒だったルッフィーニ.肖像画もちょっと陰気だ.
ルッフィーニはその後,医者の仕事は続け,哲学の問題も考えましたが,数学的にはほとんど目覚しい仕事をしていません.晩年にコーシーがルッフィーニの定理を高く評価し,また,数人のイタリア人数学者が,同国人という愛国的理由により,ルッフィーニにエールを送っていますが,ドイツやフランスの有名な数学者たちに評価されることは最後までありませんでした.
コーシーの功績
数列の収束など,厳密な解析学に貢献の大きいコーシー  ですが,対称群の研究を発展させ,近代的な群論の基礎を作りました.コーシー自身が五次方程式の問題に取り組んだわけではありませんが,方程式の問題と群論との深い関わりを考えると,この時期に群論を発展させたコーシーの功績を小さく見ることはできません.また,コーシーは敬虔なクリスチャンで,道徳的には非常に真面目な人でしたが,他人にも大変厳しく,その結果,かなり意地悪な性格として有名でした.コーシーが他人の業績を認めることは珍しく,実際,ガロアはコーシーが査読者だったため,最初の論文を無視されています.(一説には,高校生の書いた論文などには最初から目も通さず,ガロアの論文を失くしてしまったといいます.)アーベルも同じ目に遭っています.そんなコーシーですが,ルッフィーニの功績だけは高く評価し,その定理の価値も認めていたそうです.
ですが,対称群の研究を発展させ,近代的な群論の基礎を作りました.コーシー自身が五次方程式の問題に取り組んだわけではありませんが,方程式の問題と群論との深い関わりを考えると,この時期に群論を発展させたコーシーの功績を小さく見ることはできません.また,コーシーは敬虔なクリスチャンで,道徳的には非常に真面目な人でしたが,他人にも大変厳しく,その結果,かなり意地悪な性格として有名でした.コーシーが他人の業績を認めることは珍しく,実際,ガロアはコーシーが査読者だったため,最初の論文を無視されています.(一説には,高校生の書いた論文などには最初から目も通さず,ガロアの論文を失くしてしまったといいます.)アーベルも同じ目に遭っています.そんなコーシーですが,ルッフィーニの功績だけは高く評価し,その定理の価値も認めていたそうです.
アーベルからガロアへ
ルッフィーニの証明を完成させたのは,ノルウェーのアーベル(  )です.アーベルの証明は,ルッフィーニの証明とは別に考えられましたが,いまでは惜しい所まで行った先人のルッフィーニに敬意を表して,ルッフィーニ=アーベルの定理と呼ばれることもあります.とにかく,アーベルによって,『五次方程式は代数的には解けない』ということの証明が完了しました.
)です.アーベルの証明は,ルッフィーニの証明とは別に考えられましたが,いまでは惜しい所まで行った先人のルッフィーニに敬意を表して,ルッフィーニ=アーベルの定理と呼ばれることもあります.とにかく,アーベルによって,『五次方程式は代数的には解けない』ということの証明が完了しました.
アーベルは,オスロ近郊の寒村  に生まれました.いまでも,アーベルの生地であるということ以外,特に見るべきもののない村のようです.ノルウェーは当時,人も国も貧しい後進国で,教育制度も遅れており,相次ぐ戦争や飢餓によって大変な状況にありました.しかし,アーベルの天才を認めた周囲の人や王室の応援も受けて,アーベルはフランスやドイツに留学することができました.(王室の精一杯の援助も,留学生活を支えるには不十分で,赤貧の中にアーベルは徐々に健康を崩していきます.)しかし,ドイツやフランスの数学者は,この田舎の青年に冷たく,ガウス(
に生まれました.いまでも,アーベルの生地であるということ以外,特に見るべきもののない村のようです.ノルウェーは当時,人も国も貧しい後進国で,教育制度も遅れており,相次ぐ戦争や飢餓によって大変な状況にありました.しかし,アーベルの天才を認めた周囲の人や王室の応援も受けて,アーベルはフランスやドイツに留学することができました.(王室の精一杯の援助も,留学生活を支えるには不十分で,赤貧の中にアーベルは徐々に健康を崩していきます.)しかし,ドイツやフランスの数学者は,この田舎の青年に冷たく,ガウス(  )には無視され,コーシー,ルジャンドル
)には無視され,コーシー,ルジャンドル  ,ポアソン
,ポアソン  ,フーリエ(
,フーリエ(  )などにも,まったく相手にされませんでした.唯一,真面目に話を聞いてくれたのが,ベルリンのクレルレ(
)などにも,まったく相手にされませんでした.唯一,真面目に話を聞いてくれたのが,ベルリンのクレルレ(  )です.
)です.
クレルレ自身には目立った数学的業績は無いのですが,クレルレには若い有能な人材を見抜き,助力を惜しまないという美徳がありました.アーベルはドイツ語もフランス語も下手なうえ,初対面でいきなりクレルレの論文の間違いを指摘したようで,不愉快なら追い払うことも出来たはずですが,直ちにアーベルの天才を見抜いたクレルレは,自らが主宰する論文誌にアーベルの証明を載せました.アーベルの定理が世に広く知られるようになったのは,このようにクレルレの応援も無視できませんし,その意味でアーベルはルッフィーニよりも幸運でした.

アーベルはなかなかハンサムだ.性格もとても良かったらしい.
| [§] | クレルレの論文誌は 今でも 続いています.クレルレが才能を見出した数学者には,アーベルの他にヤコブ・シュタイナー(  )などがおり,また,ディリクレ( )などがおり,また,ディリクレ(  ),アイゼンシュタイン( ),アイゼンシュタイン(  ),グラスマン( ),グラスマン(    ),クンマー( ),クンマー(  ),ワイエルシュトラス( ),ワイエルシュトラス(  )なども,彼等の処女論文をクレルレの雑誌の載せています.若い才能ある人を伸ばす,という役割も非常に大事であると痛感させられます. )なども,彼等の処女論文をクレルレの雑誌の載せています.若い才能ある人を伸ばす,という役割も非常に大事であると痛感させられます. |
アーベルはその後,超越関数や楕円関数の研究を進めて大きな業績を上げますが,結核にもかかり,健康は徐々に悪化していきました.この間,画期的な超越関数の論文を,ルジャンドルには『字が読みにくい』という理由で無視され,コーシーには例によって原稿を失くされてしまったりしています.最後に,アーベルは婚約者を友人に頼み,わずか 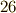 歳でこの世を去りました.(友人と婚約者は,遺言どおりアーベルの死後結婚しています.)
歳でこの世を去りました.(友人と婚約者は,遺言どおりアーベルの死後結婚しています.)
長い間,数学者を悩ませてきた五次方程式の解の公式の問題は,アーベルによって最終的に(否定的な形で)解決されたわけですが,方程式の可解性の必要十分条件を一般的に示すのが,いま勉強しているガロア理論です.ガロア理論を使い,可解群,ガロア群といった言葉を使えば,ルッフィーニやアーベルの証明ももっと簡単に,かつ,より包括的に考えることが出来ます.ガロアの劇的な人生については,またあとで触れることにします.
この後の記事の内容
この後の記事は,五次以上の代数方程式が代数的に解けないことを鮮やかに示すガロア理論の説明を中心にします.内容は意外に単純で,次のような定理を順番に証明するだけです.
- 体
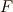 上の方程式が代数的に解けるとき,最小分解体を
上の方程式が代数的に解けるとき,最小分解体を 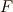 とすると,ガロア群
とすると,ガロア群 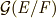 は可解群になります.
は可解群になります. - 五次以上の代数方程式では,ガロア群が可解群になりません.
もちろん,拡大体,最小分解体,ガロア群といった概念をしっかり理解していないといけませんし,可解群,正規部分群,巡回群といった群論の話題も,随時復習していきますが,大きな流れとしては一本道ですし,ここまでの記事で必要なことはほとんど出てきています.上記の定理 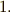 ,
, 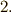 を証明するのが大まかな戦略目標だということを念頭に置きつつ,次へ進んでください.
を証明するのが大まかな戦略目標だということを念頭に置きつつ,次へ進んでください.
| [¶] | 数学には色々な理解の仕方があり,人ぞれぞれだと思いますが,人間の思考として割りと自然なのは,まず最終目標とだいたいの道筋をつかみ,後で細部を詰めていくという方法だと思います.厳密なことは数学ではとても大事ですが(そして,厳密性は数学の特長ですが),厳密になること自体が数学の目的ではありません.異論もあるとは思いますが,数学の目的は,論理の積み重ねの延長に浮かび上がってくる,まったく新しい概念を理解し,楽しむことだと思います.そのように考えれば,細かな証明を後回しにするというアプローチもあって良いと思います.(細かな証明をなおざりにしても良い,という意味ではありません.順序として後回しにするだけです.)先に結果を考えてしまって,泥縄式に間を埋めていくということになりますが,これが意外と人間の思考に沿っているような気がします.厳密な数学の教科書は,必要になる定理を順々に並べ上げ,それらを組み合わせて導ける定理を次に導き・・・,という作業を繰り返して目標に近づいていく構成になっていますが,これだと最初の段階で何を細々と証明しているのか方角を見失いやすいですし,あとから何度もページを戻って定理を参照しないといけません.さらに,最低限必要な定理以上に,派生的な定理が紹介されているような場合,とても道のりが遠く感じられ,初学者の多くが挫折してしまうように思います.ガロア理論が載っているのはほとんどが純粋な代数学の教科書であるため,特にそうした傾向が強いように思います.物理のかぎしっぽでは,とにかく『どうして五次方程式が代数的に解けないのか』を,曲がりなりにも誰でも理解できるように,先述の泥縄式アプローチで定理を証明していこうと思います.この試みがうまくいくか分かりませんが,途中で自分の立ち位置を見失わないように,あまり細かい部分にはまり込まないで読んでみて下さい.(証明の細かい部分がいい加減だという話もあります...汗) |