代数的数と超越数
一つの前の記事 代数方程式の性質 で代数方程式を定義しました.
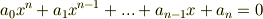
特に, 有理係数の代数方程式の解 を 代数的数 と呼びます.例えば 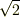 や
や 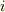 は,
は, 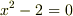 ,
, 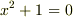 といった有理係数代数方程式の解ですから代数的数です.
といった有理係数代数方程式の解ですから代数的数です. 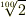 もやはり
もやはり 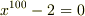 という有理係数代数方程式の解ですから代数的数です.一方,
という有理係数代数方程式の解ですから代数的数です.一方, 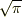 は
は 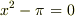 という代数方程式の解ではありますが,係数
という代数方程式の解ではありますが,係数  が有理数ではありませんので,この例を見る限り
が有理数ではありませんので,この例を見る限り 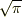 は代数的数ではありません.
は代数的数ではありません.
しかし,他に  を解とする,有理係数の代数方程式は一切存在しないと言えるのでしょうか?世の中には無限に代数方程式があるわけですから,どんな数だって,何らかの代数方程式の解になっているということないでしょうか?実は,世の中の仕組みはそうはなっていません.どうしても代数方程式の解にはならない数が無数に存在します.これらを 超越数 と呼びます.
を解とする,有理係数の代数方程式は一切存在しないと言えるのでしょうか?世の中には無限に代数方程式があるわけですから,どんな数だって,何らかの代数方程式の解になっているということないでしょうか?実は,世の中の仕組みはそうはなっていません.どうしても代数方程式の解にはならない数が無数に存在します.これらを 超越数 と呼びます.
超越数の有名な例には 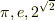 等があります.ある数が代数的数であることを証明するのは簡単ですが,超越数であることを証明するのはとても難しいことです.
等があります.ある数が代数的数であることを証明するのは簡単ですが,超越数であることを証明するのはとても難しいことです.  が超越数であることの証明は
が超越数であることの証明は 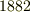 年,リンデマン(
年,リンデマン(  )によってなされましたが,とても難しいものだそうです.
)によってなされましたが,とても難しいものだそうです.

(  が超越数であることを証明したリンデマン)
が超越数であることを証明したリンデマン)
練習問題1
一般に, 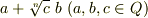 の形をした数は代数的であることを示して下さい.(ヒント:このような数を
の形をした数は代数的であることを示して下さい.(ヒント:このような数を  と置いて,移項したり累乗したりして代数方程式を作ってみましょう.)
と置いて,移項したり累乗したりして代数方程式を作ってみましょう.)
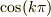 は
は 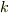 が有理数であるときに代数的数であることを示して下さい.(ヒント:加法定理を使ってみましょう.)
が有理数であるときに代数的数であることを示して下さい.(ヒント:加法定理を使ってみましょう.)