1のn乗根
方程式  の解を考えます.これは
の解を考えます.これは 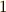 の
の 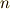 乗根で,複素数の知識を使えば,
乗根で,複素数の知識を使えば, ![\zeta = \exp [\frac{2\pi i}{n}]=\cos\frac{2\pi i}{n} + i \sin \frac{2\pi i}{n}](./1c67a612b864443bcbde9750d26e99f8.png) と表わされる数になります. 有限巡回群 の記事で見たように,この方程式の解
と表わされる数になります. 有限巡回群 の記事で見たように,この方程式の解 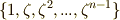 は巡回群をなします.
は巡回群をなします.
いま,  の最小分解体を
の最小分解体を 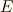 とすると,
とすると, 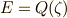 が言えますが,ガロア群
が言えますが,ガロア群 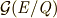 の元は
の元は  の解を置換しますので,ある適当な整数
の解を置換しますので,ある適当な整数 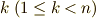 を用い,ガロア群に属する任意の元
を用い,ガロア群に属する任意の元 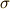 の作用は必ず次式のように書けるはずです.
の作用は必ず次式のように書けるはずです.
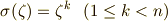
ただし,この範囲にある 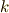 全てにおいて,
全てにおいて,  と
と 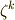 が一対一に対応するとは限りません.
が一対一に対応するとは限りません. 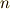 と
と 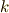 が
が 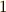 以外に公約数
以外に公約数  を持つ場合,次式が成り立つため,
を持つ場合,次式が成り立つため, 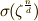 と
と 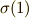 が同じになってしまいます.
が同じになってしまいます.
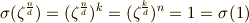
従って,一対一対応の写像が得られるのは 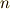 と
と 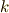 が互いに素
が互いに素 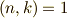 のときに限ります.
のときに限ります. 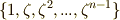 に対し,
に対し, 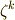 (ただし
(ただし 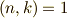 )を 1の原始n乗根 と呼びます.一般に,原始
)を 1の原始n乗根 と呼びます.一般に,原始 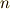 乗根は一つとは限りません.
乗根は一つとは限りません.  が
が 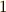 の原始
の原始 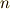 乗根となるための必要十分条件は
乗根となるための必要十分条件は 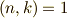 ですので,一般に
ですので,一般に 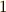 の
の 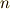 乗根は,『
乗根は,『 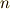 以下の整数で
以下の整数で 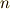 と互いに素である整数の個数』だけ存在すると言えます.
と互いに素である整数の個数』だけ存在すると言えます. 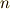 と互いに素である整数
と互いに素である整数 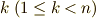 の個数は,よく
の個数は,よく 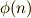 で表わされます.
で表わされます.
theorem
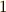 の原始
の原始 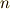 乗根は
乗根は 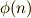 個あります.
個あります.
ここに出てきた  を オイラーのファイ関数 と呼びます.ファイ関数を使うと,
を オイラーのファイ関数 と呼びます.ファイ関数を使うと, ![|\cal G \it (E/Q)|=[Q(\zeta ):Q] \le \phi (n)](./1065226b754c18e09df8a99b35731b76.png) と書くことが出来ます.また,次の定理も重要です.
と書くことが出来ます.また,次の定理も重要です.
theorem
![\zeta = \exp [\frac{2\pi i}{n}]](./311cbb76e7b5df35e2555bd135f39636.png) の最小多項式は,
の最小多項式は, 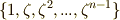 の全てを解として持ちます.
の全てを解として持ちます.
この定理の証明は長くなるので,ここでは省略します. 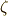 が代数方程式の解として与えられるとき,常に他の
が代数方程式の解として与えられるとき,常に他の 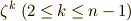 も一緒に与えられるということです.この定理により,
も一緒に与えられるということです.この定理により,  の解
の解 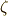 の最小多項式は
の最小多項式は 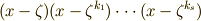 の形に書けることが要請されます.添字の
の形に書けることが要請されます.添字の 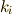 は,
は, 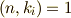 を満たす
を満たす 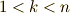 だけを取るものとします.この最小多項式を 円周等分方程式 と呼びます.円周等分方程式の解は,複素平面上で単位円の円周を等分点に当たりますから,この名前の意味は非常に明快だと思います.
だけを取るものとします.この最小多項式を 円周等分方程式 と呼びます.円周等分方程式の解は,複素平面上で単位円の円周を等分点に当たりますから,この名前の意味は非常に明快だと思います.
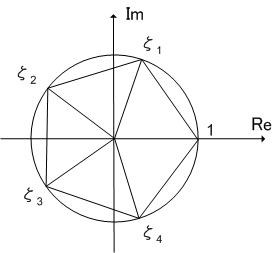
例えば  の解は複素平面上の単位円の周の五等分点にあたる.
の解は複素平面上の単位円の周の五等分点にあたる.
円周等分方程式は 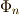 という記号で表わすことが多いようです.
という記号で表わすことが多いようです.
先ほどの定理の系として次の定理も重要です. 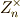 は剰余体
は剰余体 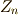 の乗法群を意味するとします.
の乗法群を意味するとします.
corollary
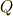 に
に 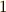 の
の 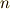 乗根
乗根 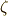 を添加した拡大体を
を添加した拡大体を 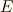 とすると,
とすると, ![[E:Q]=\phi (n)](./74febf07a45a54851815634363a376f4.png) がなりたちます.さらにガロア群
がなりたちます.さらにガロア群 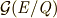 は
は 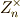 に同型となります.
に同型となります.
proof
まず先ほどの議論より ![[E:Q]=\phi (n)](./74febf07a45a54851815634363a376f4.png) となるはずですが,
となるはずですが, 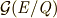 の元
の元 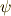 を
を 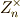 の各類
の各類 ![[k]_{n}](./f4e5b0bbe71f94856a78526bb9063900.png) に対応させる写像があれば,ガロア群
に対応させる写像があれば,ガロア群 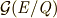 は
は 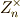 と同型になるはずです.いま
と同型になるはずです.いま 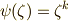 ,
, 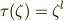 とすると,合成写像は
とすると,合成写像は 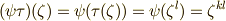 となりますので,
となりますので, ![\psi \longmapsto [k]_{n}](./85c4937e3715baa7c274cb56c8b36e26.png) ,
, ![\tau \longmapsto [l]_{n}](./dcf62b2272adb8a26776d53ecfb34e8c.png) に対して,
に対して, ![\psi \tau \longmapsto [kl]_{n}](./d1821253e95cedca15c05253eb6a42e5.png) が言え,この写像は単準同型になっています.逆に
が言え,この写像は単準同型になっています.逆に ![[k]_{n}](./f4e5b0bbe71f94856a78526bb9063900.png) から
から 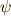 への写像も一つに決まるので,結局この写像は同型だと言えます.■
への写像も一つに決まるので,結局この写像は同型だと言えます.■
拡大体の基底に関する注意
拡大体の次数について注意です. 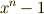 の解
の解 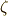 を使い,拡大体
を使い,拡大体 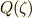 を考えます.
を考えます. 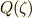 の元は,一般に
の元は,一般に 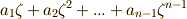 と表わされ,
と表わされ, 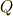 上のベクトル空間と見た場合には
上のベクトル空間と見た場合には 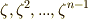 が基底を張ることになります.あれ,
が基底を張ることになります.あれ, 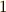 は基底に無いのでしょうか?要りません.ベクトルの足し算だと思って図形的に考えればすぐに分かりますが,
は基底に無いのでしょうか?要りません.ベクトルの足し算だと思って図形的に考えればすぐに分かりますが, 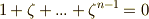 がなりたつため,
がなりたつため, 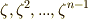 と
と 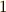 は独立ではないのです.
は独立ではないのです. 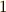 の
の 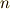 乗根を添加するとき,拡大次数を間違わないように注意して下さい.
乗根を添加するとき,拡大次数を間違わないように注意して下さい.
例えば 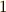 の五乗根.
の五乗根. 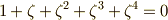 となる.
となる.
円分体
一般に 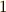 の
の 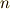 乗根を添加した拡大体を 円分体 と呼びます.(一般に,と書いたのは,標数が零ではない体上で円周等分方程式を考えることもあるからです.)いま
乗根を添加した拡大体を 円分体 と呼びます.(一般に,と書いたのは,標数が零ではない体上で円周等分方程式を考えることもあるからです.)いま 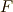 上の円周等分方程式円分体を考え,円分体
上の円周等分方程式円分体を考え,円分体 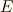 を得たとすると,
を得たとすると, 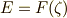 であって,
であって, 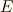 は一般に
は一般に 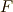 のガロア拡大体となります.
のガロア拡大体となります.
先ほど,円周等分方程式を 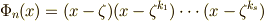 の形に書きましたが,これを次のように書き直すことも出来ます.
の形に書きましたが,これを次のように書き直すことも出来ます. 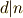 は『
は『 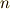 の約数
の約数  』という意味です.
』という意味です.
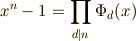
円分体は美しい代数構造を持っていますが,代数的整数論という分野で重要だそうです.かのガウスが整数論を『数学の女王』と呼んだのは有名な話ですが,整数論は数学の中でも特に難しく,かつ美しい分野です.普通の整数(有理整数)の性質を研究する分野を初等整数論と呼びますが(初等というのは簡単という意味ではありません!!),これに対して代数的整数,つまり 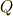 上の代数方程式の解として得られる数の性質を考える分野を代数的整数論と呼びます.
上の代数方程式の解として得られる数の性質を考える分野を代数的整数論と呼びます.
有名なフェルマーの大定理は 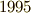 年にワイルズ(
年にワイルズ( 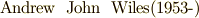 )によって証明されましたが,証明の中でもとりわけ重要な鍵を握っていた部分が,岩澤理論と呼ばれる代数的整数論の理論でした.ここまで行くと,著者も内容が分かっていないので知ったかぶりの説明は止めますが,岩澤理論とは代数体の円分
)によって証明されましたが,証明の中でもとりわけ重要な鍵を握っていた部分が,岩澤理論と呼ばれる代数的整数論の理論でした.ここまで行くと,著者も内容が分かっていないので知ったかぶりの説明は止めますが,岩澤理論とは代数体の円分 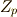 拡大(円分拡大と
拡大(円分拡大と 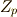 拡大を合わせたものです)と呼ばれるものの構造に関する予想です.この先には,随分と面白そうな世界が広がっているようです.
拡大を合わせたものです)と呼ばれるものの構造に関する予想です.この先には,随分と面白そうな世界が広がっているようです.
代数的整数論の分野は伝統的に日本から優秀な数学者がたくさん出ています.例えば,類体論の高木貞治  や岩澤理論の岩澤健吉(
や岩澤理論の岩澤健吉(  )が有名です.数学の分野を正確に区別は出来ませんが,代数幾何,数論幾何など,関連の深い分野もやはり日本の研究者が得意とする分野で,フィールズ賞を取った京都大学の森重文(
)が有名です.数学の分野を正確に区別は出来ませんが,代数幾何,数論幾何など,関連の深い分野もやはり日本の研究者が得意とする分野で,フィールズ賞を取った京都大学の森重文(  )などが有名でしょう.もしこの辺りの分野に興味のある人がいたら,日本で研究するにはいいかも知れません.
)などが有名でしょう.もしこの辺りの分野に興味のある人がいたら,日本で研究するにはいいかも知れません.